A good friend of mine recently discovered some of the fun things you can do with complex numbers if you’re using them to represent points in the plane. Yesterday, I re-read a passage by Tony Smith about why one should be interested in Clifford algebras. Tony Smith’s passage included all of the fun one can have with the complex plane and extends it to three, four, five, and more dimensions. I thought, I should segue from the complex numbers in the plane to Clifford algebras to quaternions in 3-space to Clifford algebras again in a series of posts here.
What are Complex Numbers
Say you’re playing around with polynomials. You start playing with the equation . WIth a little fiddling, you find this is equivalent to
. Then, you take the square root of both sides to find that
. We started with a polynomial equation in one variable in which the highest exponent was two and we found two answers.
Pounding your chest and sounding your barbaric yawp, you move on to . This should be easy, right? With the same fiddling, we find
and then
.
Uh-oh. What do we do now? We can’t think of any number that when multiplied by itself gives us a negative number. If we start with zero, we end with zero. If we multiply a positive number by itself, we get a positive number. If we multiply a negative number by itself, we get a positive number. Again!
So, how do we get around this? We pull an ace out of our sleeve. We just run with the idea that there is such a number and see where it takes us. We say, There is a number
such that
. Everything else is going to stay the same.
Where does this take us? It turns out, it takes us very, very far. For starters, our equation , a polynomial equation in one variable where the highest exponent is two, now has two answers:
.
What about ? It is a polynomial equation in one variable where the highest exponent is two. It’d be pretty spiffy if there were two answers. With the same manipulation as before, we find that
.
Now, we need to remember that if and
are positive numbers, then
. Let’s see what happens if we extend this to allow our new number
. If we said that
, then
. What happens if we multiply
? When we multiply real number
,
, and
, we can do it in any order. We could do
or
or
(or three other orders). Well, let’s assume for now that when we multiply
by a real number, we can do it in either order. Then
. That’s exactly what we were hoping it would be.
Good. Our equation is a polynomial equation in one variable where the highest exponent is two and it has two solutions
.
As it turns out, by adding in (and real number multiples of
) to our real numbers, we have the complex numbers. These complex numbers are an algebraic completion of the real numbers. That’s just a fancy way of saying that if you make a polynomial equation in one variable where all of the coefficients are real numbers and the highest exponent is
, then there will be
solutions to the equation all in the complex numbers.
[It turns out that the complex numbers are algebraically complete themselves. If you make a polynomial equation in one variable where all of the coefficients are complex numbers and the highest exponent is , then there will be
solutions to the equation in the complex numbers.]
A Quick Review of Complex Arithmetic
Above, we decided to say that is
and go from there. We also used the idea that
to find square roots of all negative numbers. And, we already played around a little bit with multiplying some numbers together. Let’s take a step back for a moment though and just add.
We still want the rest of our algebra to work. Because of that, we don’t have much choice for how imaginary numbers add together. If we take any number and add it to itself, we get
. We still want that to be true when
or
. In general, then, we will need
for any numbers
,
, and
.
Earlier, we multiplied . What if we add one to
? Well, we can definitely write this as
just like we can add one to two by just writing
. In the latter case, we already have a name for
. We could instead write
.
We don’t already have a name for . How do we know? Well, let us assume that
is some real number or some real number times
. If it is some real number, we should get a positive real number when we square it. If it is a real number times
, we should get a negative real number when we square it. But, if we multiply
(using the old
Firsts, Outers, Inners, Lasts
method), we get which is not a positive real number or a negative real number.
As it happens, all of our complex numbers will have the form: for some real numbers
and
. When we go to add two numbers together, we just add the corresponding pieces:
.
For a complex number , we call
the
real part
and the
imaginary part
. When we add two complex numbers, we add the real parts together and we add the imaginary parts together. Subtraction, likewise, goes by part. If we want , we subtract the real parts and subtract the imaginary parts to obtain
.
When we multiply two numbers together, we do it like we did with above with the FOIL method.
. We rearrange the orders of some of the bits as we did with
above to get:
. And since
, we have:
Transforming the Plane
You’ll notice above that a complex number is made up of two real numbers (and, of course, ). Every point in the plane has two real numbers as coordinates. We can co-opt the real numbers in the complex number to use as coordinates for points in the plane. If our points are:
,
,
,
, then we can represent them as complex numbers with
,
,
,
.
We can plot these just as we would their normal coordinates if we put the real part on the x-axis and the imaginary part on the y-axis. This is called an Argand Diagram.
Suppose now we want to translate all of our points by five units along the x-axis and negative two units along the y-axis. We can simply let and then add this to each of our points so that
.
Imagine instead that we want to scale the plane radially out from the origin by a factor of three. We can simply multiply each of our points by so that
. If we want to scale outward from
instead, we could translate by
, scale by
, and then translate
back.
Suppose now that we’d like to rotate the plane by some angle around the origin. For that rotation, a point
should get rotated to the point
. That is to say: the complex number
should get rotated to the complex number
.
Let’s look back to our equation for multiplying two complex numbers:
We can see the similarity to the rotation. If we take , then we get precisely:
.
The points are the points on the unit circle centered at the origin. So, if we want to rotate all of our points by an angle
around the origin, we simply have to multiply them by the point on the unit circle that is at angle
around the origin from the x-axis:
so that
. Again, if we want to rotate around the point
, we simply translate by
, rotate by
, and translate
back again.
So, now we can translate points in the plane with complex addition (or subtraction). We can scale points in the plane by multiplying by a real number. We can rotate the plane by multiplying by a complex number.
Conformal maps
There are some other transformations that naturally arise from complex arithmetic. A conformal transform is one that keeps angles constant. All of the transformations we’ve done above are conformal. If you translate the whole plane, the angles between lines are unchanged. If you scale the whole plane, the angles between lines are unchanged. If you rotate the whole plane, the angles between lines are unchanged.
As it happens, a transformation of the complex plane is a conformal map if and only if the transformation has a (complex) derivative everywhere and that derivative is non-zero everywhere. Without getting into complex derivatives here, suffice it to say, they’re pretty much just like real derivatives for simple polynomials. Let’s look at our cases above. The derivative of translating by is
which exists everywhere and is non-zero everywhere. The derivative of multiplying by
(or
) is
(or
). This exists everywhere and is non-zero everywhere (if anywhere).
Another conformal transformation of the complex plane is the Möbius transformation. The Möbius transformations preserve angles where lines meet, but they generally turn lines into curves. The Möbius transformations are of the form: for complex numbers
,
,
, and
(so long as
). You can see the Möbius transform in action on YouTube.
What’s next
Next, we’re going to see how Clifford algebras can represent all we have done here. But, that is for another day.

This was a fun read– have you checked out the website khanacademy.org? The guy on there is amazing at explaining basic math stuff.
I haven’t seen that site. I will check it out.
Thanks…
[…] numbers can be used to represent coordinates in the plane and how, once you’ve done that, complex arithmetic leads naturally to rotations, scalings, and translations of the plane. Today, we’re going to do the same with the Clifford algebra […]
[…] using complex numbers for rotating, translating, and scaling the plane […]
To obtain the roots of the complex number a+ib you take the arcotangent below 90 degrees of the complex ratio a/b and then divide by the root required. The cotangent of the result will give one of the roots of the complex ratio. For the other roots you add 360 degrees and then 720 degrees on to the arcotangent. In this way all n nth integer roots of complex numbers can be obtained.
Further to my comment of 21 May 2011, the complex number a+ib can be converted into an imaginary number by making a equal 0, and then substituting the Cotes format cos90+isin90 equalling 0+i. It will be recognised that cos180+isin180 equals -1, and cos360+isin360 equals i to the power of 4 which is +1. The same principle also applies for division
cos45+isin45 equals the square root of i. In this way the roots and powers of i, -i, +1 and -1 can be calculated all based on the Cotes format.
I refer to the last sentence of my comments of 21 May 2011. ‘In this way all n nth integer roots of complex numbers can be obtained’. This indicates that it is not possible for there to be more than n nth roots of a complex number. This has enormous implications for Hamilton’s quaternion equation i^2=j^2=k^2=ijk=-1 where -1 seems to have three square roots i,j, and k, where k seems to be wrong.
It is not possible for a number to have three square roots in the Complex numbers. But, the quaternions are not in tge complex numbers. In fact, there are infinitely many ways to map subsets of the quaternions down to the complex numbers. Note, to that ij = -ji in the quaternions whereas all complex numbers commute under multiplication.
There is no law of arithmetic which makes ij equal to anything but +1.
I agree with you if we are talking about arithmetic for real numbers and complex numbers. We are not though. We are talking about something altogether different.
This is not a statement about arithmetic. It is a statement about geometry formalized with notation that makes it look like arithmetic. If it helps, think of them just as 4-dimensional vectors: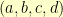 that add just like vectors add:
that add just like vectors add: 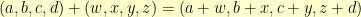 . But, unlike vectors, they can also be multiplied to create new vectors. The multiplication is such that:
. But, unlike vectors, they can also be multiplied to create new vectors. The multiplication is such that:
And, any other product can be determined if we agree that this multiplication distributes over addition just like we’re used to. So,
There are at least three ways of measuring a 90 degree rotation, firstly by multiples of the 90 degrees consisting of 90, 180, 270 and 360 etc, secondly by powers of i, being i,-1,-i, and +1 etc. Thirdly by changing the signs and positions of the coordinates (+a,+b), (+b,-a,) (-a,-b),
(-b,+a), and (+a,+b) etc. It is important not to confuse these three ways of measuring a 90 degree rotation. These three ways can be applied to a three dimensional sphere as well as to a two dimensional circle. Four dimensions are not needed.
Certainly, for 90-degree rotations (in 2D or 3D (around world axes)) you don’t need any of the artifice that I’m suggesting in this series. This series was building toward being able to rotate arbitrary-dimensional objects by arbitrary amounts. You can do that with just Euler matrices, but they’re coordinate-system dependent in a way that Clifford algebras are not.
The angle theta in your comment on Transforming the Plane is confusing. You say that theta is the angle of rotation, whereas it is the arcotangent of the ratio of the coordinates a/b. It is of course possible for it to be both, but for demonstration purposes these angles should be different.