I was pondering the Phony Physics again as I set to work on my iPhone app.
In the previous post, I twiddled the equations for damped spring motion until I found something visually pleasing. Last night, I went back to the drawing (a.k.a. white
) board.
What if I used an exponential spiral (parameterized by arc length). Then, I could easily adjust the number of times it bounces back and forth. I could use a spiral like  and
and 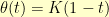 where
where 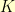 is some multiple of
is some multiple of 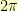 . Then, I could walk along the spiral getting to the origin when
. Then, I could walk along the spiral getting to the origin when 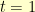 going around the origin
going around the origin 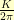 times in the process. If I follow the curve at a fixed rate, then I guarantee that my oscillations will pick up speed as I approach the origin.
times in the process. If I follow the curve at a fixed rate, then I guarantee that my oscillations will pick up speed as I approach the origin.
Rather than have it spiral into the center, I am just using the x-coordinate of the spiral as my new 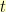 value to interpolate with. I like the effect for the most part. It overshoots a little bit far on the first oscillation. I may tweak it some more before it’s all over. For now though, I am sticking with it.
value to interpolate with. I like the effect for the most part. It overshoots a little bit far on the first oscillation. I may tweak it some more before it’s all over. For now though, I am sticking with it.
I will post some graphs soon.


