Alright, I wasn’t the first. But, I wasn’t particularly expecting to find them either.
One nascent game concept that I have in my head requires me to do some constrained shuffling. As an example constraint, imagine that you need to shuffle a deck of cards while ensuring that no card moved more than five spots away from where it started. Or, imagine that you had to shuffle the deck so that a card of rank  could only move to spot that had been held by a card of rank
could only move to spot that had been held by a card of rank 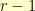 ,
,  , or
, or 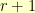 .
.
In the general case, you have a directed graph with vertexes 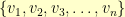 and a permutation
and a permutation 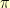 such that
such that 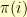 can only equal
can only equal 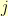 if there is an edge in the graph from
if there is an edge in the graph from 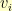 to
to 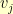 .
.
Well, as this is for a game, it would get pretty boring if there were only a few possible shuffles. On the other hand, if there are a large number of possible shuffles, then I haven’t really restricted the shuffling at all for all practical purposes. So, then the question is: for a given directed graph, how many possible shuffles are there? Can I generate them without generating any of the invalid permutations, too?
Today, I started with the How many?
-question. I started with a very simple graph. The vertexes are spaced evenly along an east-west line. Each vertex is connected only to itself, its nearest neighbor to the east, and its nearest neighbor to the west. Put another way, 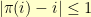 for
for ![i \in [1,n] i \in [1,n]](http://l.wordpress.com/latex.php?latex=i%20%5Cin%20%5B1%2Cn%5D&bg=FFFFCC&fg=000000&s=0) .
.
Let’s say we already had a row of 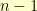 vertexes. If we add another vertex at the beginning of the row, then there are two things that a shuffle can do to that new vertex: leave it where it is or swap it with what had been the first vertex in the row. Now, suppose that
vertexes. If we add another vertex at the beginning of the row, then there are two things that a shuffle can do to that new vertex: leave it where it is or swap it with what had been the first vertex in the row. Now, suppose that 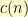 is the count of valid shuffles for
is the count of valid shuffles for 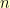 vertexes in this configuration. The case where our new vertex stays where it is leaves
vertexes in this configuration. The case where our new vertex stays where it is leaves 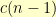 possibilities for the rest of the row. The case where our new vertex swaps places with the old first vertex leaves
possibilities for the rest of the row. The case where our new vertex swaps places with the old first vertex leaves 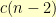 possibilities. As such,
possibilities. As such, 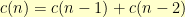 .
.
Cha-ching. Note that 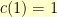 and
and 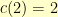 , then
, then 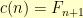 where
where 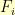 are the Fibonacci numbers.
are the Fibonacci numbers.
Things get a great deal messier if we move up to 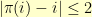 . More on that some other time…
. More on that some other time…
