A month ago, a friend posted the following problem on Facebook. I just noticed it this week.
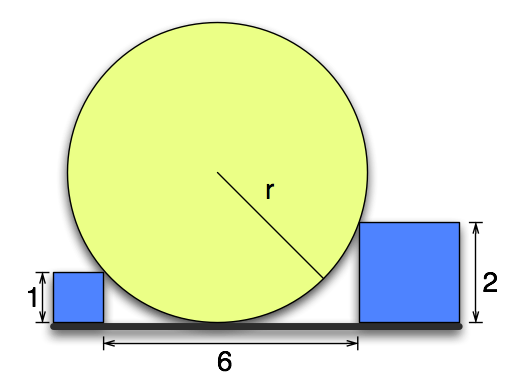
The goal is to find the exact length of the radius  .
.
I love this kind of math problem. Â It has a bunch of features that make it a great, toy math problem.
- It looks like it’s going to be easy, but at the same time seems at a glance to not have enough information
- It looks like a geometry problem but only requires that you know:
- All radii of a circle have the same length
- A radius to a point where a tangent line touches the circle is perpendicular to that tangent line
- It requires only very basic algebra:
- Pythagorean theorem
- Solving quadratics
- The numbers in the problem are small, non-zero integers
I spent the next 25 minutes and six pieces of paper working the problem. About 20% of the time that I spent was rechecking my work. Why did I bother rechecking my work on a toy problem?
Warning: Spoilers ahead. If you like this kind of problem, stop reading now and play with it first.
The problem with the problem
This problem failed to satisfy one of my other criterion for great, toy puzzle problems.
- The answer is a small natural number (or the current year)
I am notorious for messing up signs when doing large algebra calculations. I had to check and recheck all of my work to make sure that I hadn’t done 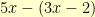 and gotten
and gotten 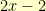 somewhere. If I had come up with an integer value for
somewhere. If I had come up with an integer value for  , I’d have been done. Instead, the answer involved a half-integer plus a multiple of
, I’d have been done. Instead, the answer involved a half-integer plus a multiple of 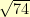 .
.
What? 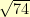 ?!? Raise your hand if you’ve ever seen that written anywhere before this problem.
?!? Raise your hand if you’ve ever seen that written anywhere before this problem.
That’s what I thought.
So, I spent the next hour looking for a different set of numbers to put in for 1, 2, and 6 so that the radius  would come out to an integer. My approach was Brownian, at best. I threw Pythagorean triples at a wall until one stuck.
would come out to an integer. My approach was Brownian, at best. I threw Pythagorean triples at a wall until one stuck.
The sticky triple left me with ![[50,200,360] [50,200,360]](http://l.wordpress.com/latex.php?latex=%5B50%2C200%2C360%5D&bg=FFFFCC&fg=000000&s=0) to put in place of
to put in place of ![[1,2,6] [1,2,6]](http://l.wordpress.com/latex.php?latex=%5B1%2C2%2C6%5D&bg=FFFFCC&fg=000000&s=0) . So, I put the problem down for awhile.
. So, I put the problem down for awhile.
The next time that I was in the car, I realized that the radius for the sticky triple was less than 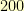 . That meant that the larger box was touching the upper half of the circle instead of the lower half. The circle had to overlap the box.
. That meant that the larger box was touching the upper half of the circle instead of the lower half. The circle had to overlap the box.
So, I was back to the drawing board. Of course, I’d have been back to the drawing board at some point anyway because that sticky triple violated both of my small numbers criteria.
Warning: If you want to play around with finding a set of numbers that work, do it before you read the following. There are even more spoilers ahead.
Infinitely many combinations to get an integer radius
When I next sat down to play (pronounced: /OBSESS/) with this problem, I quickly hit upon the following way to take any Pythagorean triple 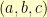 and make a version of the above puzzle where the radius
and make a version of the above puzzle where the radius  is an integer.
is an integer.
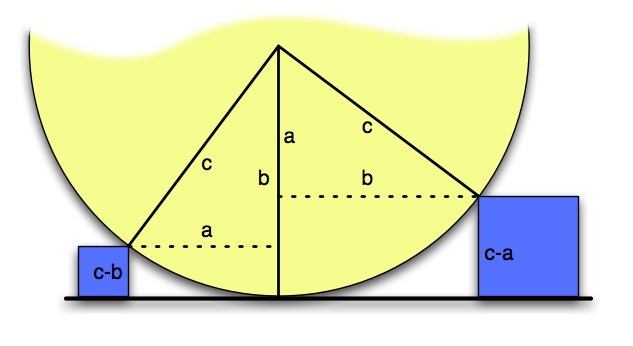
In fact, using a 3-4-5 triangle, it is obvious that had the distance between the blocks in the original problem been 7 instead of 6, the radius would have been a small natural number.
Now. Now, I had infinitely many ways to construct this problem so that the radius was an integer. But, did I have all of the ways?
All your configuration are belong to us
When looking at that last diagram, the first question that comes to mind (for me) is: Do I really need to use the same Pythagorean triple on the left and right triangles?
The answer, of course, is No.
If I have two Pythagorean triples 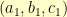 and
and 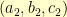 and
and 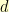 is any (positive) divisor of both
is any (positive) divisor of both 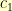 and
and 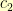 , then I can start with an
, then I can start with an 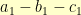 triangle on the left and an
triangle on the left and an 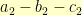 triangle on the right. I can then scale up the left triangle by
triangle on the right. I can then scale up the left triangle by 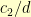 and scale the right triangle up by
and scale the right triangle up by 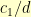 . Now, both triangles have the same hypotenuse.
. Now, both triangles have the same hypotenuse.
This means that if the left block has height  , the right block has height
, the right block has height  , the distance between the two blocks is
, the distance between the two blocks is 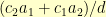 , and the resulting circle has radius
, and the resulting circle has radius 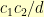 .
.
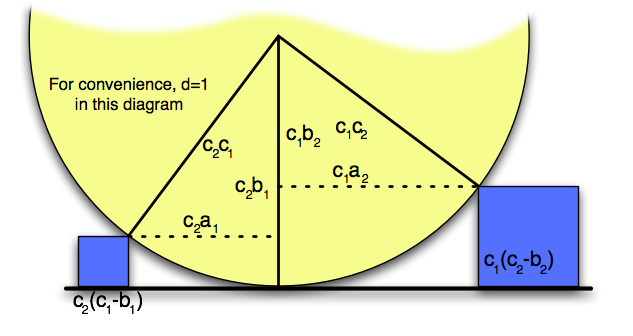
Does this cover all of the solutions? Could I possibly have non-integer 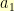 and
and 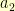 such that
such that 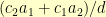 is still integer?
is still integer?
Well, for the problem to be formulated entirely with integers, we certainly need the hypotenuse of the right triangles to be an integer. Further, to make the blocks integer heights then both of the legs of the right triangles along the vertical radius must also be integer. So, if the triangle on the left had hypotenuse  , vertical leg
, vertical leg  and horizontal leg
and horizontal leg  , then we know that
, then we know that 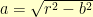 where both
where both  and
and  are integers. Thus,
are integers. Thus,  must be the square root of an integer.
must be the square root of an integer.
It is easy to see that if  were a non-integer rational number, then its square would also be a non-integer rational number. So, either
were a non-integer rational number, then its square would also be a non-integer rational number. So, either  is integer or it is the irrational square root of an integer.
is integer or it is the irrational square root of an integer.
So, can  be an irrational number? If
be an irrational number? If  were an irrational number, then the horizontal leg of the other triangle would have to be some integer
were an irrational number, then the horizontal leg of the other triangle would have to be some integer 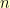 minus the irrational
minus the irrational  for the distance between the two blocks to be an integer. Let’s say the vertical leg of the triangle on the right is
for the distance between the two blocks to be an integer. Let’s say the vertical leg of the triangle on the right is 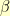 . Just like
. Just like  in the first triangle,
in the first triangle, 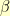 must be an integer. We also know that
must be an integer. We also know that 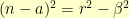 . This, in turn, means that
. This, in turn, means that 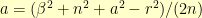 . The right hand side is clearly rational, so
. The right hand side is clearly rational, so  could not have been irrational.
could not have been irrational.
So, there you have it: all of the numbers that make this problem have all integers on the drawing and an integer answer.



