A friend showed me this about 15 years ago. I use it every time I need to calculate the variance of some data set. I always forget the exact details and have to derive it again. But, it’s easy enough to derive that it’s never a problem.
I had to derive it again on Friday and thought, I should make sure more people get this tool into their utility belts
.
First, a quick refresher on what we’re talking about here. The mean 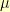 of a data set
of a data set 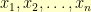 is defined to be
is defined to be 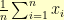 . The variance
. The variance 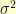 is defined to be
is defined to be 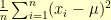 .
.
A naïve approach to calculating the variance then goes something like this:
(defun mean-variance (data)
(flet ((square (x) (* x x)))
(let* ((n (length data))
(sum (reduce #'+ data :initial-value 0))
(mu (/ sum n))
(vv (reduce #'(lambda (accum xi)
(+ accum (square (- xi mu))))
data :initial-value 0)))
(values mu (/ vv n)))))
This code runs through the data list once to count the items, once to calculate the mean, and once to calculate the variance. It is easy to see how we could count the items at the same time we are summing them. It is not as obvious how we can calculate the sum of squared terms involving the mean until we’ve calculated the mean.
If we expand the squared term and pull the constant 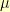 outside of the summations it ends up in, we find that:
outside of the summations it ends up in, we find that:
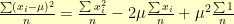
When we recognize that 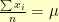 and
and 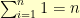 , we get:
, we get:
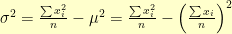
.
This leads to the following code:
(defun mean-variance (data)
(flet ((square (x) (* x x)))
(destructuring-bind (n xs x2s)
(reduce #'(lambda (accum xi)
(list (1+ (first accum))
(+ (second accum) xi)
(+ (third accum) (square xi))))
data :initial-value '(0 0 0))
(let ((mu (/ xs n)))
(values mu (- (/ x2s n) (square mu)))))))
The code is not as simple, but you gain a great deal of flexibility. You can easily convert the above concept to continuously track the mean and variance as you iterate through an input stream. You do not have to keep data around to iterate through later. You can deal with things one sample at a time.
The same concept extends to higher-order moments, too.
Happy counting.
Edit: As many have pointed out, this isn’t the most numerically stable way to do this calculation. For my part, I was doing it with Lisp integers, so I’ve got all of the stability I could ever want. 🙂 But, yes…. if you are intending to use these numbers for big-time decision making, you probably want to look up a really stable algorithm.