Speedy iPhone App Programming February 4th, 2010
Patrick Stein

Sunday, I decided that I needed a simpler statistics tracking program to keep track of stuff while I’m coaching volleyball. I started out keeping them on paper, but felt that I was staring at the page too often to find where to put a tick mark.

Next, I tried the iVolleyStats Match iPhone app. It is pretty reasonable to use, but it’s got too many controls on the user-interface. The only way that I could keep up with a match was to forgo half of the functionality… either ignoring who is getting credit for an act, ignoring passing stats altogether, and not recording attack or block attempts at all.

For the past few weeks, I have tried using the Voice Memos application on the iPhone. I narrate the game into my phone as the game goes on. This lets me get really fine resolution of statistics, but it doesn’t give me any information in real-time. When I call a time-out, I am going from memory to say how we’ve been passing or hitting. This takes away the lion’s share of the benefit one gets from gathering statistics at all.

So, my team has a tournament this Saturday. I decided Sunday night that I should try to get together an iPhone app that does what I want. I’ve long been thinking about what I want in a volleyball stat tracking iPhone app. What I want will be a big, big undertaking (read: longer than one week). So, I started studying Apple’s CoreData APIs on Sunday night and Monday morning. Then, I dove in.

Now, my previous application was based upon Cocos2D-iPhone. As such, it didn’t involve any of the Apple UIKit classes or any work with Interface Builder. This application is navigation based with table views and custom table view cells from separate NIB files.

Despite this being my first real foray into the UIKit and CoreData APIs, I’ve got an application that I can use on Saturday. There are two more bits that I will try to add tomorrow, but that I don’t need for Saturday. To package it up for sale, there’s more functionality that I’ll need to add in case you don’t like things in the order that I have them on the screen or in case you want to add your own categories of statistic. And, I need to make some specialized visualization screens for some of the stats.

The screenshot here is the main stat-tracking interface. The stats present are Penn State’s stats from my trial run watching game one of their NCAA semifinal against Hawaii from last December. In retrospect, I think I probably gave them credit for two neutral attacks that I should have called free balls. Other than that, I think it’s pretty good. It’s definitely information that will do me well during time-outs.

I fought for a long time this morning trying to get my UIBarButtonItem to show up in my UINavigationBar for one screen. It turns out that these two methods don’t quite do the same thing on iPhoneOS 3.1.2:

// working version that shows my UIBarButton in the UINavigationBar
- (void)showStatTrackingScreen {
    [navigationController setViewControllers:[NSArray arrayWithObject:homeViewController] animated:NO];
    [navigationController pushViewController:trackStatsController animated:YES];
}

// version made of fail that does NOT show my UIBarButton in the UINavigationBar
// until you go forward a screen and pop back to this one.
- (void)showStatTrackingScreenMadeOfFail {
    [navigationController setViewControllers:[NSArray arrayWithObjects:homeViewController,
                                                                       trackStatsController,
                                                                       nil]
                                    animated:YES];
}

Spelling iPhone App sent to Beta Testers January 28th, 2010
Patrick Stein

I am pleased to say that I just sent my first iPhone app out to some friends to beta test. I expect to forward it along to Apple for inclusion in the App Store some time in the next week or two.

At this point, I am far more comfortable with Objective-C and the Cocoa class hierarchy than I was even a month ago. I still think Objective-C is awful. You take a nice functional Smalltalk-ish language, you throw away most of the functional, you pretend like you have garbage collection when you don’t, you strip out any form of execution control, you add some funky compiler pragma-looking things (including one called synthesize that only fabricates about half of what you’d want it to build), you change the semantics of ->, and then you interleave it with C! Wahoo! Instant headache!

But, after I found the for-each sort of construction, my code got quite a bit simpler. A whole bunch of loops like this:

NSEnumerator* ee = [myArray enumerator];
MyItem* item;
while ( ( item = (MyItem*)[ee nextObject] ) != nil ) {
   ...
}

went to this:

for ( MyItem* item in myArrayOrEnumerator ) {
   ...
}

Casting to Integers Considered Harmful August 6th, 2009
Patrick Stein

Background

Many years back, I wrote some ambient music generation code. The basic structure of the code is this: Take one queen and twenty or so drones in a thirty-two dimensional space. Give them each random positions and velocities. Limit the velocity and acceleration of the queen more than you limit the same for the drones. Now, select some point at random for the queen to target. Have the queen accelerate toward that target. Have the drones accelerate toward the queen. Use the average distance from the drones to the queens in the i-th dimension as the volume of the i-th note where the notes are logarithmically spaced across one octave. Clip negative volumes to zero. Every so often, or when the queen gets close to the target, give the queen a new target.

It makes for some interesting ambient noise that sounds a bit like movie space noises where the lumbering enemy battleship is looming in orbit as its center portion spins to create artificial gravity within.

I started working on an iPhone application based on this code. The original code was in C++. The conversion to Objective C was fairly straightforward and fairly painless (as I used the opportunity to try to correct my own faults by breaking things out into separate functions more often).

Visualization troubles

uniform
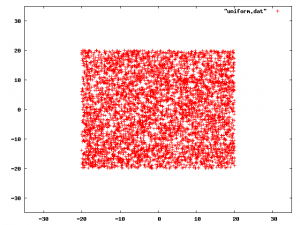
The original code though chose random positions and velocities from uniform distributions. The iPhone app is going to involve visualization as well as auralization. The picture at the right here is a plot of five thousand points with each coordinate selected from a uniform distribution with range [-20,+20]. Because each axis value is chosen independently, it looks very unnatural.

gauss
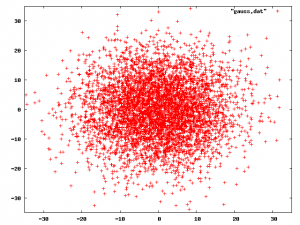
What to do? The obvious answer is to use Gaussian random variables instead of uniform ones. The picture at the right here is five thousand points with each coordinate selected from a Gaussian distribution with a standard-deviation of 10. As you can see, this is much more natural looking.

How did I generate the Gaussians?

I have usually used the Box-Muller method of generating two Gaussian-distributed random variables given two uniformly-distributed random variables:

(defun random-gaussian ()
  (let ((u1 (random 1.0))
        (u2 (random 1.0)))
    (let ((mag (sqrt (* -2.0 (log u1))))
          (ang (* 2.0 pi u2)))
      (values (* mag (cos ang))
              (* mag (sin ang))))))

But, I found an article online that shows a more numerically stable version:

(defun random-gaussian ()
  (flet ((pick-in-circle ()
           (loop as u1 = (random 1.0)
                as u2 = (random 1.0)
                as mag-squared = (+ (* u1 u1) (* u2 u2))
                when (< mag-squared 1.0)
                return (values u1 u2 mag-squared))))
    (multiple-value-bind (u1 u2 mag-squared) (pick-in-circle)
      (let ((ww (sqrt (/ (* -2.0 (log mag-squared)) mag-squared))))
        (values (* u1 ww)
                (* u2 ww))))))

For a quick sanity check, I thought, let’s just make sure it looks like a Gaussian. Here, I showed the code in Lisp, but the original code was in Objective-C. I figured, If I just change the function declaration, I can plop this into a short C program, run a few thousand trials into some histogram buckets, and see what I get.

The trouble with zero

So, here comes the problem with zero. I had the following main loop:

#define BUCKET_COUNT 33
#define STDDEV       8.0
#define ITERATIONS   100000

  for ( ii=0; ii < ITERATIONS; ++ii ) {
    int bb = val_to_bucket( STDDEV * gaussian() );
    if ( 0 <= bb && bb < BUCKET_COUNT ) {
      ++buckets[ bb ];
    }
  }

I now present you with three different implementations of the val_to_bucket() function.

int val_to_bucket( double _val ) {
  return (int)_val + ( BUCKET_COUNT / 2 );
}

int val_to_bucket( double _val ) {
  return (int)( _val + (int)( BUCKET_COUNT / 2 ) );
}

int val_to_bucket( double _val ) {
  return (int)( _val + (int)( BUCKET_COUNT / 2 ) + 1 ) - 1;
}

As you can probably guess, after years or reading trick questions, only the last one actually works as far as my main loop is concerned. Why? Every number between -1 and +1 becomes zero when you cast the double to an integer. That’s twice as big a range as any other integer gets. So, for the first implementation, the middle bucket has about twice as many things in it as it should. For the second implementation, the first bucket has more things in it than it should. For the final implementation, the non-existent bucket before the first one is the overloaded bucket. In the end, I used this implementation instead so that I wouldn’t even bias non-existent buckets:

int val_to_bucket( double _val ) {
  return (int)lround(_val) + ( BUCKET_COUNT / 2 );
}

Programming When Clarity Counts May 5th, 2009
Patrick Stein

In my previous post, I wrote some code in Perl because I wanted the code to be clear and obvious. Wait? What? Who uses Perl when they want clarity?

Perl

I admit: I was surprised myself. Seriously, I tried several other languages first. Let’s just focus on the first loop here. Here’s the Perl again for reference:

my $total = 0.0;
foreach my $item ( @list_of_items ) {
    $total += weight( $item );
}

Objective C

The actual code that I was attempting to explain was in Objective C with the NeXTStep foundation classes. I couldn’t imagine that anyone would want to try to understand it:

double total = 0.0;
NSEnumerator* ee = [itemList objectEnumerator];
Item* item;
while ( ( item = (Item*)[ee nextObject] ) != nil ) {
    total += [item weight];
}

C

My first attempt for the article was to write it in C using an array of items.

double total = 0.0;
unsigned int ii;
for ( ii = 0; ii < itemCount; ++ii ) {
    total += weight( itemArray[ ii ] );
}

That’s not too terrible. There is, however, a great deal of syntax and code devoted to handling the array including an extra variable to track its length. Beyond that, the loop counter is of little use to someone trying to understand the concept.

C++

My next go was C++. My hope was that iterators would make the looping less painful. C++ iterators, however, are the very model of pain.

double total = 0.0;
std::list< Item* >::const_iterator it;
for ( it = itemList.begin(); it != itemList.end(); ++it ) {
    total += weight( *it );
}

This requires the reader to wade through a syntactic thicket to get the iterator into the picture at all. It also requires a certain comfort with pointers that one wouldn’t have coming from another language.

Java

My next attempt was Java. I hate Java. It may not be terrible for this code with the new looping constructs that came in Java 1.5. Alas, I quit coding it before I made it through this first loop.

Lisp

Of course, I wanted to code this in Lisp:

(let ((total (reduce #'+ list-of-items :key #'weight)))
   ...)

That would be perfectly clear to someone who has used Lisp or Scheme. Alas, not everyone has.

So… Perl…

If you want to write the Perl code, you have to understand the difference between scalars and arrays. To read the code, however, you don’t have to grok that distinction to see what’s going on. I didn’t try it in Python. Maybe it would be clear to a wider audience. I may have to try it next time.

Sapir-Whorf with Programming Languages February 12th, 2009
Patrick Stein

I’ve been coding in Objective-C for a month or so now. It is interesting (in a Sapir-Whorf sort of way), how the language changes the way that I code. Switching from Objective-C to Lisp made me notice something that I hadn’t really noticed when moving from C++/Java/Perl to Lisp.

In Lisp, I will pull something out into a separate function if it makes the current function more self-contained, more one idea. In C++, I will only pull something out into a separate function if I need the same functionality in multiple places.

Actually, it’s even worse than that in C++. For stuff that is less than six or so lines, I might maintain it in several functions. Or, if I’m using some Literate Programming tool, I will just use the same chunk in multiple places. The notable exception in C++ is when I want to use something as a loop conditional, I may bother to break it out into its
own function:

while ( incrementCounter( cntr, min, max, dimensions ) ) {
    // body of loop here
}

In C++ or Objective-C, I might do something like this:

// some portion of my function

unsigned int choice = random() % length;
void* currentChoice = options[ choice ];
    // yes, I know I can memcpy(), but that's not as obvious
for ( unsigned int ii=choice+1; ii < length; ++ii ) {
    options[ ii-1 ] = options[ ii ];
}
--length;

// some code using currentChoice

In Lisp, I would never consider keeping that code inline. I would put it in another function right away.

This, this is one of the things I meant when I said Lisp is just plain fun. It’s easy to make a new function. I can just do it. I don’t have to fret too much over the name. I don’t have to fret too much over the argument
list. I don’t have to pre-declare it in this header file with the same signature as that implementation file. I
don’t have to pretend its a method when it’s really just a function. I can return multiple values if I need to do so. I don’t have to worry much about which compilation units will need to see this to compile.

Part of the maze generation code that I wrote in Objective-C needs to track walls. I don’t need the same structure during generation that I will use once it’s generated. So, I have a Wall class declared. It feels wrong to declare it right in the header file for the Maze. It feels silly to break it out into its own header file. What I should be doing is making a separate MazeFactory and have its implementation include the declaration of this Wall class. But, that is such overkill here. I just want the darn maze.

In Lisp, I would just be done with no feelings of guilt at all.

Updates In Email

Email:

RSS Feeds

l