For an application that I’m working on, I needed a way to scale quantities that range (theoretically) over the real numbers (though practically are probably between plus and minus three) into positive numbers. I wanted the function to be everywhere increasing, I wanted 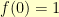 , and I wanted control of the derivative at
, and I wanted control of the derivative at 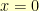 .
.
The easy choice is: 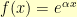 . This is monotonically increasing.
. This is monotonically increasing. 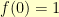 and
and 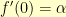 .
.
I needed to scale three such quantities and mush them together. I thought it’d be spiffy then to have three different functions that satisfy my criteria. The next logical choice was 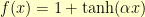 . It is everywhere positive and increasing. And, it has
. It is everywhere positive and increasing. And, it has 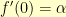 .
.
Now, I needed third function that was always positive, always increasing, had 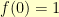 and
and 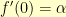 . One choice was:
. One choice was: 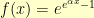 . But, that seemed like overkill. It also meant that I really had to keep my
. But, that seemed like overkill. It also meant that I really had to keep my 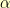 tiny if I didn’t want to scale things into the stratosphere.
tiny if I didn’t want to scale things into the stratosphere.
Playing with hyperbolas
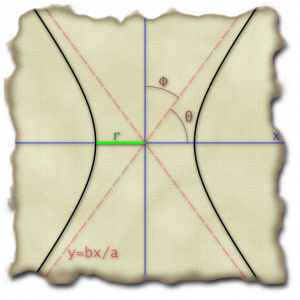 So, I thought… why don’t I make a hyperbola, rotate it, and shift it so that the apex of one side of the hyperbola is at
So, I thought… why don’t I make a hyperbola, rotate it, and shift it so that the apex of one side of the hyperbola is at 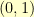 . And, I can adjust the parameters of the hyperbola so that
. And, I can adjust the parameters of the hyperbola so that 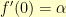 . After a variety of false starts where I tried to keep the hyperbola general until the very end (
. After a variety of false starts where I tried to keep the hyperbola general until the very end (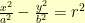 , rotated by
, rotated by 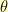 degrees, and shifted by
degrees, and shifted by 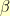 ), I quickly got bogged down in six or seven incredibly ugly equations in eight or nine variables.
), I quickly got bogged down in six or seven incredibly ugly equations in eight or nine variables.
So, it was time to start trying to make it easy from the beginning. I noticed that if was going to rotate it by an angle 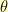 in the clockwise direction, then I needed
in the clockwise direction, then I needed 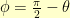 to be such that
to be such that 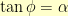 if my slope was going to work out right in the end.
if my slope was going to work out right in the end.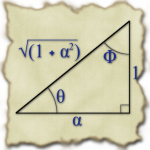 So, I’m looking at the basic triangle on the right then to determine all of my sines and cosines and such.
So, I’m looking at the basic triangle on the right then to determine all of my sines and cosines and such.
Based on that triangle, it was also obvious that the asymptote for my starting hyperbola had to have 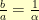 . I played around a bit then with making
. I played around a bit then with making 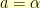 and
and 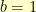 . In the end, I found things simplified sooner if I started with
. In the end, I found things simplified sooner if I started with 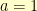 and
and  .
.
I also needed  to be such that the point
to be such that the point 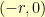 rotate up so that its
rotate up so that its 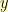 -coordinate was
-coordinate was 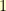 . This meant that
. This meant that 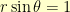 or
or  .
.
So, my starting hyperbola then was: 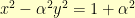 .
.
From there, I had to rotate the  and
and 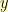 by
by 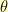 in the clockwise direction. This gave me:
in the clockwise direction. This gave me:
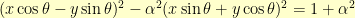
A little multiplying out leads to:
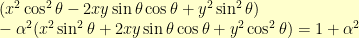
From there, using 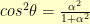 ,
, 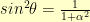 , and
, and 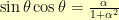 , we come to:
, we come to:
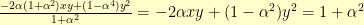
The only step remaining was to shift it all over so that when 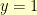 , we end up with
, we end up with 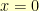 . Plugging in
. Plugging in 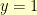 , we see that
, we see that 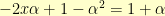 . That equation balances when
. That equation balances when 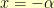 . We want it to balance when
. We want it to balance when 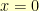 , so we’re going to substitute
, so we’re going to substitute  in place of the
in place of the  in the above equation to get:
in the above equation to get:
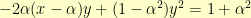
We can easily verify that the point 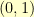 is on the curve. And, we can implicitly differentiate the above to get:
is on the curve. And, we can implicitly differentiate the above to get:
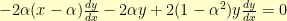
Plopping
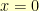
and
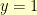
in there, we find that
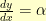
.
This is pretty good as it goes. The only step is to complete the square to find a nicer expression for 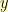 in terms of
in terms of  . We start by adding
. We start by adding ![\left[ \frac{\alpha}{\sqrt{1 - \alpha^2}} (x - \alpha) \right]^2 \left[ \frac{\alpha}{\sqrt{1 - \alpha^2}} (x - \alpha) \right]^2](http://l.wordpress.com/latex.php?latex=%5Cleft%5B%20%5Cfrac%7B%5Calpha%7D%7B%5Csqrt%7B1%20-%20%5Calpha%5E2%7D%7D%20%28x%20-%20%5Calpha%29%20%5Cright%5D%5E2&bg=FFFFCC&fg=000000&s=0) to both sides to get:
to both sides to get:
![\left[ \sqrt(1 - \alpha^2)y - \frac{\alpha}{\sqrt{1 - \alpha^2}(x - \alpha)} \right]^2 = 1 + \alpha^2 + \frac{\alpha}{1 - \alpha^2} (x-\alpha)^2 \left[ \sqrt(1 - \alpha^2)y - \frac{\alpha}{\sqrt{1 - \alpha^2}(x - \alpha)} \right]^2 = 1 + \alpha^2 + \frac{\alpha}{1 - \alpha^2} (x-\alpha)^2](http://l.wordpress.com/latex.php?latex=%5Cleft%5B%20%5Csqrt%281%20-%20%5Calpha%5E2%29y%20-%20%5Cfrac%7B%5Calpha%7D%7B%5Csqrt%7B1%20-%20%5Calpha%5E2%7D%28x%20-%20%5Calpha%29%7D%20%5Cright%5D%5E2%20%3D%201%20%2B%20%5Calpha%5E2%20%2B%20%5Cfrac%7B%5Calpha%7D%7B1%20-%20%5Calpha%5E2%7D%20%28x-%5Calpha%29%5E2&bg=FFFFCC&fg=000000&s=0)
This is easy enough to solve for 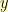 by taking the square root of both sides and shuffling some things about:
by taking the square root of both sides and shuffling some things about:
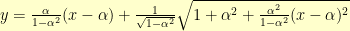
Here are all three curves with 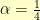 . The exponential is in black, the hyperbolic tangent is in red, and the hyperbola is in blue:
. The exponential is in black, the hyperbolic tangent is in red, and the hyperbola is in blue:
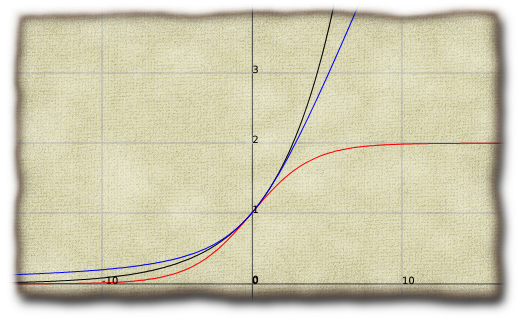
The first image on the page here was made with Zach’s Vecto library with some post-processing in the GIMP. (Here is the source file: hyperbola.lisp.) The second image was made entirely within the GIMP. And, the last image was made using Foo Plot and the GIMP.