Finding the Perfect Hyperbola February 15th, 2010
Patrick Stein

For an application that I’m working on, I needed a way to scale quantities that range (theoretically) over the real numbers (though practically are probably between plus and minus three) into positive numbers. I wanted the function to be everywhere increasing, I wanted f(0) = 1, and I wanted control of the derivative at x = 0.

The easy choice is: f(x) = e^{\alpha x}. This is monotonically increasing. f(0) = 1 and f^\prime(0) = \alpha.

I needed to scale three such quantities and mush them together. I thought it’d be spiffy then to have three different functions that satisfy my criteria. The next logical choice was f(x) = 1 + \mathrm{tanh} (\alpha x). It is everywhere positive and increasing. And, it has f^\prime(0) = \alpha.

Now, I needed third function that was always positive, always increasing, had f(0) = 1 and f^\prime(0) = \alpha. One choice was: f(x) = e^{e^{\alpha x} - 1}. But, that seemed like overkill. It also meant that I really had to keep my \alpha tiny if I didn’t want to scale things into the stratosphere.

Playing with hyperbolas

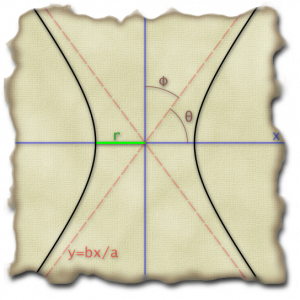So, I thought… why don’t I make a hyperbola, rotate it, and shift it so that the apex of one side of the hyperbola is at (0,1). And, I can adjust the parameters of the hyperbola so that f'(0) = \alpha. After a variety of false starts where I tried to keep the hyperbola general until the very end (\frac{x^2}{a^2} - \frac{y^2}{b^2} = r^2, rotated by \theta degrees, and shifted by \beta), I quickly got bogged down in six or seven incredibly ugly equations in eight or nine variables.

So, it was time to start trying to make it easy from the beginning. I noticed that if was going to rotate it by an angle \theta in the clockwise direction, then I needed \phi = \frac{\pi}{2} - \theta to be such that \tan \phi = \alpha if my slope was going to work out right in the end. 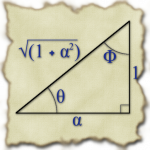So, I’m looking at the basic triangle on the right then to determine all of my sines and cosines and such.

Based on that triangle, it was also obvious that the asymptote for my starting hyperbola had to have \frac{b}{a} = \frac{1}{\alpha}. I played around a bit then with making a = \alpha and b = 1. In the end, I found things simplified sooner if I started with a = 1 and b = \frac{1}{\alpha}.

I also needed r to be such that the point (-r,0) rotate up so that its y-coordinate was 1. This meant that r \sin \theta = 1 or r = \frac{1}{\sin \theta} = \sqrt{1 + \alpha^2}.

So, my starting hyperbola then was: x^2 - \alpha^2 y^2 = 1 + \alpha^2.

From there, I had to rotate the x and y by \theta in the clockwise direction. This gave me:

(x\cos\theta - y\sin\theta)^2 - \alpha^2 (x\sin\theta + y\cos\theta)^2 = 1 + \alpha^2

A little multiplying out leads to:

(x^2\cos^2\theta - 2xy\sin\theta\cos\theta + y^2\sin^2\theta) \\ - \alpha^2(x^2\sin^2\theta + 2xy\sin\theta\cos\theta + y^2\cos^2\theta) = 1 + \alpha^2

From there, using cos^2\theta = \frac{\alpha^2}{1 + \alpha^2}, sin^2\theta = \frac{1}{1 + \alpha^2}, and \sin\theta\cos\theta = \frac{\alpha}{1 + \alpha^2}, we come to:

\frac{-2\alpha(1 + \alpha^2)xy + ( 1 - \alpha^4 )y^2}{1 + \alpha^2} = -2\alpha{}xy + (1 - \alpha^2)y^2 = 1 + \alpha^2

The only step remaining was to shift it all over so that when y = 1, we end up with x = 0. Plugging in y = 1, we see that -2x\alpha + 1 - \alpha^2 = 1 + \alpha. That equation balances when x = -\alpha. We want it to balance when x = 0, so we’re going to substitute (x - \alpha) in place of the x in the above equation to get:

-2\alpha(x - \alpha)y + (1 - \alpha^2)y^2 = 1 + \alpha^2

We can easily verify that the point (0,1) is on the curve. And, we can implicitly differentiate the above to get:

-2\alpha(x - \alpha)\frac{dy}{dx} - 2\alpha{}y + 2(1 - \alpha^2)y\frac{dy}{dx} = 0

Plopping x = 0 and y = 1 in there, we find that \frac{dy}{dx} = \alpha.

This is pretty good as it goes. The only step is to complete the square to find a nicer expression for y in terms of x. We start by adding \left[ \frac{\alpha}{\sqrt{1 - \alpha^2}} (x - \alpha) \right]^2 to both sides to get:

\left[ \sqrt(1 - \alpha^2)y - \frac{\alpha}{\sqrt{1 - \alpha^2}(x - \alpha)} \right]^2 = 1 + \alpha^2 + \frac{\alpha}{1 - \alpha^2} (x-\alpha)^2

This is easy enough to solve for y by taking the square root of both sides and shuffling some things about:

y = \frac{\alpha}{1 - \alpha^2}(x - \alpha) + \frac{1}{\sqrt{1 - \alpha^2}} \sqrt{1 + \alpha^2 + \frac{\alpha^2}{1 - \alpha^2}(x - \alpha)^2}

Here are all three curves with \alpha = \frac{1}{4}. The exponential is in black, the hyperbolic tangent is in red, and the hyperbola is in blue:

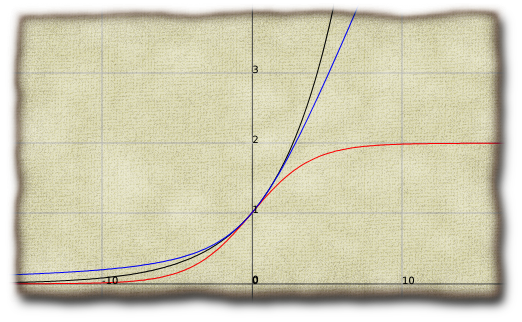
The first image on the page here was made with Zach’s Vecto library with some post-processing in the GIMP. (Here is the source file: hyperbola.lisp.) The second image was made entirely within the GIMP. And, the last image was made using Foo Plot and the GIMP.

RSS Feeds

l