Galois fields are used in a number of different ways. For example, the AES encryption standard uses them.
Arithmetic in Galois Fields
The Galois fields of size  for various
for various 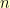 are convenient in computer applications because of how nicely they fit into bytes or words on the machine. The Galois field
are convenient in computer applications because of how nicely they fit into bytes or words on the machine. The Galois field 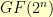 has
has 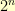 elements. These elements are represented as polynomials of degree less than
elements. These elements are represented as polynomials of degree less than 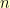 with all coefficients either 0 or 1. So, to encode an element of
with all coefficients either 0 or 1. So, to encode an element of 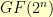 as a number, you need an
as a number, you need an 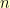 -bit binary number.
-bit binary number.
For example, let us consider the Galois field 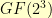 . It has
. It has 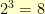 elements. They are (as binary integers)
elements. They are (as binary integers) 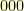 ,
, 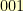 ,
, 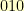 ,
, 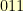 ,
, 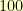 ,
, 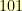 ,
, 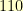 , and
, and 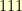 . The element
. The element 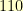 , for example, stands for the polynomial
, for example, stands for the polynomial 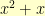 . The element
. The element 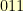 stands for the polynomial
stands for the polynomial 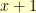 .
.
The coefficients add together just like the integers-modulo-2 add. In group theory terms, the coefficients are from 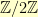 . That means that
. That means that 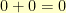 ,
, 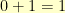 ,
, 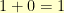 , and
, and 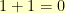 . In computer terms,
. In computer terms, 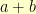 is simply
is simply  XOR
XOR  . That means, to get the integer representation of the sum of two elements, we simply have to do the bitwise-XOR of their integer representations. Every processor that I’ve ever seen has built-in instructions to do this. Most computer languages support bitwise-XOR operations. In Lisp, the bitwise-XOR of
. That means, to get the integer representation of the sum of two elements, we simply have to do the bitwise-XOR of their integer representations. Every processor that I’ve ever seen has built-in instructions to do this. Most computer languages support bitwise-XOR operations. In Lisp, the bitwise-XOR of  and
and  is
is (logxor a b).
Multiplication is somewhat trickier. Here, we have to multiply the polynomials together. For example, 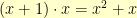 . But, if we did
. But, if we did 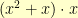 , we’d end up with
, we’d end up with 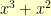 . We wanted everything to be polynomials of degree less than
. We wanted everything to be polynomials of degree less than 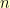 and our
and our 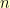 is 3. So, what do we do?
is 3. So, what do we do?
What we do, is we take some polynomial of degree 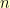 that cannot be written as the product of two polynomials of less than degree
that cannot be written as the product of two polynomials of less than degree 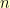 . For our example, let’s use
. For our example, let’s use 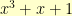 (which is
(which is 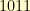 in our binary scheme). Now, we need to take our products modulo this polynomial.
in our binary scheme). Now, we need to take our products modulo this polynomial.
You may not have divided polynomials by other polynomials before. It’s a perfectly possible thing to do. When we divide a positive integer  by another positive integer
by another positive integer  (with
(with  bigger than 1), we get some answer strictly smaller than
bigger than 1), we get some answer strictly smaller than  with a remainder strictly smaller than
with a remainder strictly smaller than  . When we divide a polynomial of degree
. When we divide a polynomial of degree 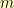 by a polynomial of degree
by a polynomial of degree 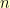 (with
(with 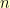 greater than zero), we get an answer that is a polynomial of degree strictly less than
greater than zero), we get an answer that is a polynomial of degree strictly less than 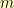 and a remainder that is a polynomial of degree strictly less than
and a remainder that is a polynomial of degree strictly less than 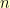 .
.
Dividing proceeds much as long division of integers does. For example, if we take the polynomial (with integer coefficients) 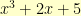 and divide it by the polynomial
and divide it by the polynomial 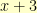 , we start by writing it as:
, we start by writing it as:
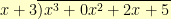
We notice that to get
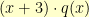
to start with
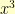
, we need
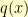
to start with
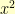
. We then proceed to subtract
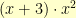
and then figure out that we need a
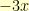
for the next term, and so on. We end up with
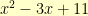
with a remainder of
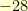
(a degree zero polynomial).

For the example we cited earlier we had
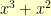
which we needed to take modulo
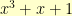
. Well, dividing
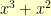
by
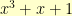
, we see that it goes in one time with a remainder of
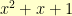
. [Note: addition and subtraction are the same in
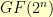
.]

For a reasonable way to accomplish this in the special case of our integer representations of polynomials in
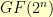
, see this article about
Finite Field Arithmetic and Reed Solomon Codes. In (tail-call style) Lisp, that algorithm for
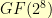
might look something like this to multiply

times

modulo
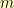
:
(flet ((next-a (a)
(ash a -1))
(next-b (b)
(let ((overflow (plusp (logand b #x80))))
(if overflow
(mod (logxor (ash b 1) m) #x100)
(ash b 1)))))
(labels ((mult (a b r)
(cond
((zerop a) r)
((oddp a) (mult (next-a a) (next-b b) (logxor r b)))
(t (mult (next-a a) (next-b b) r)))))
(mult a b 0)))
How is the Galois field structured?
The additive structure is simple. Using our 8-bit representations of elements of 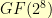 , we can create an image where the pixel in the
, we can create an image where the pixel in the  -th row and
-th row and 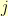 -th column is the sum (in the Galois field) of
-th column is the sum (in the Galois field) of  and
and 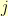 (written as binary numbers). That looks like this:
(written as binary numbers). That looks like this:

Just before the
above-mentioned article hit
reddit, I got to wondering if the structure of the Galois field was affected at all by the choice of polynomial you used as the modulus. So, I put together some code to try out all of the polynomials of order 8.
Remember way back at the beginning of multiplication, I said that the modulus polynomial had to be one which couldn’t be written as the product of two polynomials of smaller degree? If you allow that, then you have two non-zero polynomials that when multiplied together will equal your modulus polynomial. Just like with integers, if you’ve got an exact multiple of the modulus, the remainder is zero. We don’t want to be able to multiply together two non-zero elements to get zero. Such elements would be called zero divisors.
Zero divisors would make these just be Galois rings instead of Galois fields. Another way of saying this is that in a field, the non-zero elements form a group under multiplication. If they don’t, but multiplication is still associative and distributes over addition, we call it a ring instead of a field.
Galois rings might be interesting in their own right, but they’re not good for AES-type encryption. In AES-type encryption, we’re trying to mix around the bits of the message. If our mixing takes us to zero, we can never undo that mixing—there is nothing we can multiply or divide by to get back what we mixed in.
So, we need a polynomial that cannot be factored into two smaller polynomials. Such a polynomial is said to be irreducible. We can just start building an image for the multiplication for a given modulus and bail out if it has two non-zero elements that multiply together to get zero. So, I did this for all elements which when written in our binary notation form odd numbers between (and including) 100000001 and 111111111 (shown as binary). These are the only numbers which could possibly represent irreducible polynomials of degree 8. The even numbers are easy to throw out because they can be written as  times a degree 7 polynomial.
times a degree 7 polynomial.
The ones that worked were: 100011011, 100011101, 100101011, 100101101, 100111001, 100111111, 101001101, 101011111, 101100011, 101100101, 101101001, 101110001, 101110111, 101111011, 110000111, 110001011, 110001101, 110011111, 110100011, 110101001, 110110001, 110111101, 111000011, 111001111, 111010111, 111011101, 111100111, 111110011, 111110101, and 111111001. That first one that worked (100011011) is the one used in AES. Its multiplication table looks like:

Here’s it is again on the left with the multiplication table when 110011111 is the modulus on the right:


So, the addition image provides some insight into how addition works. The multiplication tables, at least for me, provide very little insight into anything. They don’t even make a good stereo pair.
To say two of the multiplication tables have the same structure, means there is some way to map back and forth between them so that the multiplication still works. If we have table 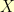 and table
and table 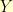 , then we need an invertible function
, then we need an invertible function 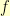 such that
such that 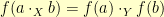 for all
for all  and
and  in the table
in the table 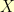 .
.
What’s next?
If there is an invertible map between two multiplication tables and there is some element  in the first table, you can take successive powers of it:
in the first table, you can take successive powers of it:  ,
, 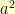 ,
, 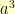 ,
,  . There are only
. There are only 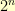 elements in
elements in 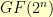 no matter which polynomial we pick. So, somewhere in there, you have to start repeating. In fact, you have to get back to
no matter which polynomial we pick. So, somewhere in there, you have to start repeating. In fact, you have to get back to  . There is some smallest, positive integer
. There is some smallest, positive integer 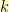 so that
so that 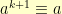 in
in 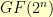 . If we pick
. If we pick 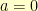 , then we simply have that
, then we simply have that 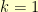 . For non-zero
. For non-zero  , we are even better off because
, we are even better off because 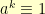 .
.
So, what if I took the powers of each element of 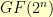 in turn? For each number, I would get a sequence of its powers. If I throw away the order of that sequence and just consider it a set, then I would end up with a subset of
in turn? For each number, I would get a sequence of its powers. If I throw away the order of that sequence and just consider it a set, then I would end up with a subset of 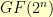 for each
for each  in
in 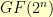 . How many different subsets will I end up with? Will there be a different subset for each
. How many different subsets will I end up with? Will there be a different subset for each  ?
?
I mentioned earlier that the non-zero elements of 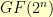 form what’s called a group. The subset created by the powers of any fixed
form what’s called a group. The subset created by the powers of any fixed  forms what’s called a subgroup. A subgroup is a subset of a group such that given any two members of that subset, their product (in the whole group) is also a member of the subset. As it turns out, for groups with a finite number of elements, the number of items in a subgroup has to divide evenly into the number of elements in the whole group.
forms what’s called a subgroup. A subgroup is a subset of a group such that given any two members of that subset, their product (in the whole group) is also a member of the subset. As it turns out, for groups with a finite number of elements, the number of items in a subgroup has to divide evenly into the number of elements in the whole group.
The element zero in 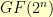 forms the subset containing only zero. The non-zero elements of
forms the subset containing only zero. The non-zero elements of 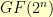 form a group of
form a group of 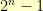 elements. The number
elements. The number 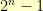 is odd (for all
is odd (for all 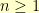 ). So, immediately, we know that all of the subsets we generate are going to have an odd number of items in them. For
). So, immediately, we know that all of the subsets we generate are going to have an odd number of items in them. For 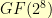 , there are 255 non-zero elements. The numbers that divide 255 are: 1, 3, 5, 15, 17, 51, 85, and 255.
, there are 255 non-zero elements. The numbers that divide 255 are: 1, 3, 5, 15, 17, 51, 85, and 255.
It turns out that the non-zero elements of 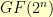 form what’s called a cyclic group. That means that there is at least one element
form what’s called a cyclic group. That means that there is at least one element  whose subset is all
whose subset is all 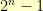 of the non-zero elements. If take one of those
of the non-zero elements. If take one of those  ‘s in
‘s in 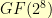 whose subset is all 255 of the elements, we can quickly see that the powers of
whose subset is all 255 of the elements, we can quickly see that the powers of 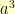 form a subset containing 85 elements, the powers of
form a subset containing 85 elements, the powers of 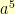 form a subset containing 51 elements, …, the powers of
form a subset containing 51 elements, …, the powers of 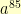 form a subset containing 3 elements, and the powers of
form a subset containing 3 elements, and the powers of 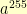 form a subset containing 1 element. Further, if both
form a subset containing 1 element. Further, if both  and
and  have all 255 elements in their subset, then
have all 255 elements in their subset, then  and
and 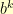 will have the same number of elements in their subsets for all
will have the same number of elements in their subsets for all 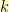 . We would still have to check to make sure that if
. We would still have to check to make sure that if 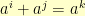 that
that 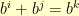 to verify the whole field structure is the same.
to verify the whole field structure is the same.
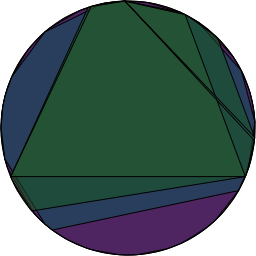
This means there are only 8 different subset of 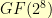 ‘s non-zero elements which form subgroups. Pictorially, if we placed the powers of
‘s non-zero elements which form subgroups. Pictorially, if we placed the powers of  around a circle so that
around a circle so that 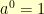 was at the top and the powers progressed around the circle and then drew a polygon connecting consecutive points, then consecutive points in the
was at the top and the powers progressed around the circle and then drew a polygon connecting consecutive points, then consecutive points in the 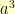 sequence and consecutive points in the
sequence and consecutive points in the 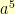 sequence, etc…. we’d end up with this:
sequence, etc…. we’d end up with this:
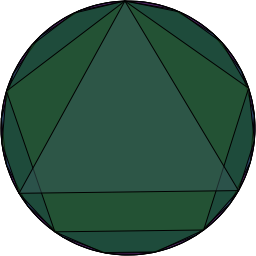
If we don’t reorder them and just leave them in the numerical order of their binary representation, the result isn’t as aesthetically pleasing as the previous picture. Here are the same two we used before 100011011 (on the left) and 110011111 (on the right). They are easier to look at. They do not lend much more insight nor make a better stereo pair.
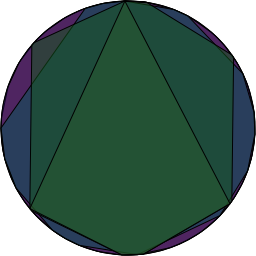
*shrug* Here’s the source file that I used to generate all of these images with
Vecto and
ZPNG:
group.lisp