nklein software

When you see pictures of the Mandelbrot set you are seeing the results of iterating a function over and over.

For the Mandelbrot set, you take a complex number . You square it and add the original number. You take that, square it, and add the original. You do this a number of times. If the value stays relatively close to zero, the number is in the Mandelbrot set. If the value takes off away from zero, the number is not in the Mandelbrot set. Typically, one colors in the parts of the picture that aren’t in the Mandelbrot set with some color that indicates just how fast it hightailed it out of there.

I wanted to try something different. I wanted to see what the iteration process looks like. So, I threw together some code using Lisp with cl-opengl.

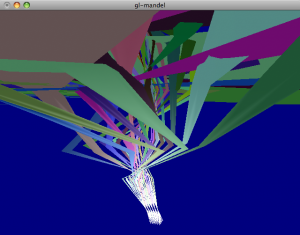The first visualization that I coded was to start with tiny patches of the complex plane. From each patch, I would extrude it up out of the plane and over to its next iteration. The picture at the right is (IIRC) a patch with side-length one half centered at with either 25 or 36 patches tiled in that area. As you can see, this isn’t a wholly satisfying picture of what’s going on.

The other idea that I had was to show the progress through iterations as an animation. This is a bit more interesting to look at until some of the patches start overflowing my floating point numbers or get too big for my clipping region. This is an area of side-length one centered at the origin with four-hundred patches. Here is a movie of that flow.