Exponential Spirals for Game Effects ⇐

Exponential Spirals for Game Effects May 4th, 2009
Patrick Stein

In earlier posts, I mentioned finding polynomials, riffing off of damped harmonic motion, and then hitting on exponential spirals all trying to come up with a nice looking way to snap game tiles back into place when they are released. I want them to overshoot and then settle into place rather than snap directly into their spot.

The Basic Spiral

I am talking about a simple spiral of the form:

$\theta(t) = Kt$ $r(t) = \alpha\left(Kt\right)^{n}$ for some integer $n$ .

That would be an equation for a spiral that starts at the origin and heads outward as $t$ increases. For my application though, I want to end at the origin so I need to substitute $1-t$ in for $t$ .

$\theta(t) = K(1-t)$ $r(t) = \alpha\left(K(1-t)\right)^{n}$

The math is also going to work out slightly better if I use $n-2$ in place of $n$ in the above equations:

$\theta(t) = K(1-t)$ $r(t) = \alpha\left(K(1-t)\right)^{n-2}$

I don’t want the piece to spiral into place when released though. So, really, I am concerned with just the $x$ coordinate from the above equations:

$x(t) = r(t) \cos \theta(t) = \alpha K^{n-2} (1-t)^{n-2} \cos \left(K\left(1-t\right)\right)$

To normalize everything, I am going to let $\alpha = K^{2-n}$ . And, since I want my interpolation value to go from zero to one instead of one to zero, I am again going to subtract this all from one:

$x(t) = 1 - (1-t)^{n-2} \cos \left(K\left(1-t\right)\right)$

Parametrizing by Arc Length

If I just plot the spiral as is, then I am stuck with the same problem that I had with damped spring motion: the frequency is constant. The rate at which it would shimmy would not increase. I want it to really settle into place. So, I have to walk through the spiral at a fixed rate. I need to rescale the $(1-t)$ into something else so that for any given time interval, I cover the same arc length on the spiral.

The first step then is to figure out how much arc length I sweep out with any given $t$ . Call this arc length $s(t)$ :

$s(t) = \int_0^{t} r(\tau) \theta(\tau) d\theta = \int_0^{t} - \alpha K^{n} (1 - \tau)^{n-1} d\tau$ which comes out to: $s(t) = \frac{\alpha K^n}{n} \left(\left(1-t\right)^n-1\right)$

Then, to rescale my $t$ , I want to use $t'$ instead so that $t' = \frac{s(t)}{s(1)}$ . So, when $t' = \frac{1}{4}$ , for example, I will need to find the $t$ such that the arc length covered in the first $t$ seconds is $\frac{1}{4}$ -th of the arc length covered in the whole interval. Solving for $t$ in the equation $t' = \frac{s(t)}{s(1)}$ comes out to:

$t = 1 - \sqrt[n]{1-t'}$

Plugging all of that back into the equation for $x(t)$ gives me:

$x(t) = 1 - \sqrt[n]{(1-t)^{n-2}} \cos \left(K\sqrt[n]{1-t}\right)$
The simplest spiral here has $n = 3$ , and we will go around four times with $K = 8\pi$ :

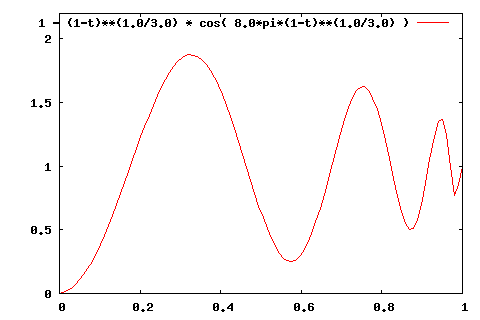
You can see how the period speeds up toward the end. This was a good starting point. However, the first oscillation goes almost as far beyond the target as our initial point was. So, I upped the exponent to $n = 9.5$ :

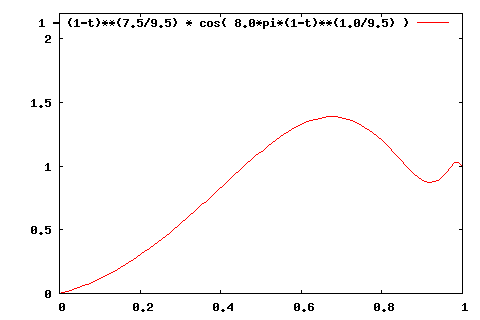
This was pretty much the effect I wanted. Unfortunately, it involves taking an $7.5$ -th power, an $9.5$ -th root, and a cosine of calculation. I decided that $\frac{7.5}{9.5}$ was close enough to one to give it a whirl without needing the $7.5$ -th power.

$x(t) = 1 - (1-t) \cos \left(K\sqrt[n]{1-t}\right)$

Here you can see the final result.

nklein software

software development and consulting