The role-playing game Paranoia was set in a dystopian future where a paranoid computer had seized control to protect us from Commie, mutant traitors. In the game, secret societies were strictly forbidden. As such, every character was a member of some secret society or other. One of those secret societies was the FCCCP: First Church of Christ, Computer Programmer. This, of course, tickled me. Heck, it still does.
Outside the world of role-playing games, there is a long tradition of analyzing sacred texts, pulling out every possible thread of meaning and applying those meanings to every aspect of life. I’ve been pondering a series of articles that combines the exegesis with the computer programming.
Well, this week’s sermon at our synagogue was about the verse Numbers 30:2:
If a man makes a vow to the LORD, or swears an oath to bind himself by some agreement, he shall not break his word; he shall do according to all that proceeds out of his mouth.
How could I sit there without pondering Programming by Contract
? In fact, I would say that this verse goes much beyond just the contract. Every line of code makes promises. Are they promises the code can keep?
To ground the discussion, I dug around for a short function that I wrote more than a year ago. The following snippet of code takes two arrays: counter and maximum. The array elements of each are assumed to be integers. The arrays are assumed to be the same length. The value of the i-th entry in counter is assumed to be less than the i-th entry in maximum. If you think of an axis-aligned, n-dimensional cube with one corner at the origin and its opposite corner at the maximum, the goal is for counter to scan through every set of integer coordinates in the cube (well, including the faces that touch the origin, but not including the faces that touch the maximum). If every entry in maximum is  , then the result should be just like incrementing a base
, then the result should be just like incrementing a base  number that is displayed least-significant digit first. If maximum were
number that is displayed least-significant digit first. If maximum were 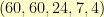 , the counter would count out the seconds in February (non-leap year).
, the counter would count out the seconds in February (non-leap year).
(defun increment-counter (counter maximum)
(unless (null counter)
(let ((nn (length counter)))
(let ((result (make-array nn :initial-contents counter)))
(dotimes (ii nn nil)
(when (< (incf (aref result ii)) (aref maximum ii))
(return result))
(setf (aref result ii) 0))))))
What promises does the above code make? The function name increment-counter is a pretty obvious promise. The function is going to increment some sort of counter. Given just the function name, what would we expect? I would expect that it takes a single argument, that argument is a reference to an integer, and that integer is incremented in place. I would be way off. Our promise is already on sketchy grounds. I’m not coming up with a particularly good name at the moment though: step-cube-walker? increment-n-dimensional-counter?
The function doesn’t increment the counter in place. Instead, it returns a newly allocated counter (or nil, if we’ve reached the end). The function declaration doesn’t make any promise that maximum will be left untouched, though Lisp doesn’t make it easy to declare that. Lisp usually handles that sort of thing by convention. The function declaration also makes no claim that the counter and maximum arguments should be arrays, let alone that they should be the same length. (Technically, the code only requires that maximum be an array. Counter can be any sequence. Further, maximum is allowed to be longer than counter, but cannot be shorter.)
Line 2 of the code doesn’t trust you to stop calling it when you’re already done. This is an interesting hedge, but not really an oath. It may rise to that level at some point though if enough code starts to depend on this utterance.
Lines 3 & 4 are the only uses of (a non-nil) counter. They work just fine for any sequence. As such, while this function always returns either nil or an array, it will accept any sequence as the counter.
Line 5 outright promises that the function is going to return nil. This is, of course, countermanded on line 7. I suppose this is akin to verses 3, 4, & 5:
[3] Or if a woman makes a vow to the LORD, and binds herself by some agreement while in her fatherâs house in her youth, [4] and her father hears her vow and the agreement by which she has bound herself, and her father holds his peace, then all her vows shall stand, and every agreement with which she has bound herself shall stand. [5] But if her father overrules her on the day that he hears, then none of her vows nor her agreements by which she has bound herself shall stand; and the LORD will release her, because her father overruled her.
Even though the loop on line five is released of its promise, it still feels like a cheap back door.
So, you can see that even in these eight lines of code, I have made many, many inadvertent promises. Hopefully, in future code, I will keep a more careful tongue.
 For a month now, I have wanted to turn that joke into a
For a month now, I have wanted to turn that joke into a