Introduction
SICP has a few sections devoted to using a general, damped fixed-point iteration to solve square roots and then nth-roots. The Functional Programming In Scala course that I did on Coursera did the same exercise (at least as far as square roots go).
The idea goes like this. Say that I want to find the square root of five. I am looking then for some number  so that
so that 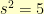 . This means that I’m looking for some number
. This means that I’m looking for some number  so that
so that 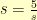 . So, if I had a function
. So, if I had a function 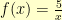 and I could find some point
and I could find some point  where
where 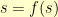 , I’d be done. Such a point is called a fixed point of
, I’d be done. Such a point is called a fixed point of 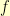 .
.
There is a general method by which one can find a fixed point of an arbitrary function. If you type some random number into a calculator and hit the “COS” button over and over, your calculator is eventually going to get stuck at 0.739085…. What happens is that you are doing a recurrence where 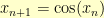 . Eventually, you end up at a point where
. Eventually, you end up at a point where 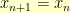 (to the limits of your calculator’s precision/display). After that, your stuck. You’ve found a fixed point. No matter how much you iterate, you’re going to be stuck in the same spot.
(to the limits of your calculator’s precision/display). After that, your stuck. You’ve found a fixed point. No matter how much you iterate, you’re going to be stuck in the same spot.
Now, there are some situations where you might end up in an oscillation where 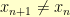 , but
, but 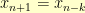 for some
for some 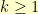 . To avoid that, one usually does the iteration
. To avoid that, one usually does the iteration 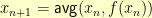 for some averaging function
for some averaging function 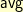 . This “damps” the oscillation.
. This “damps” the oscillation.
The Fixed Point higher-order function
In languages with first-class functions, it is easy to write a higher-order function called fixed-point that takes a function and iterates (with damping) to find a fixed point. In SICP and the Scala course mentioned above, the fixed-point function was written recursively.
(defun fixed-point (fn &optional (initial-guess 1) (tolerance 1e-8))
(labels ((close-enough? (v1 v2)
(<= (abs (- v1 v2)) tolerance))
(average (v1 v2)
(/ (+ v1 v2) 2))
(try (guess)
(let ((next (funcall fn guess)))
(cond
((close-enough? guess next) next)
(t (try (average guess next)))))))
(try (* initial-guess 1d0))))
It is easy to express the recursion there iteratively instead if that’s easier for you to see/think about.
(defun fixed-point (fn &optional (initial-guess 1) (tolerance 1e-8))
(flet ((close-enough? (v1 v2)
(<= (abs (- v1 v2)) tolerance))
(average (v1 v2)
(/ (+ v1 v2) 2)))
(loop :for guess = (* initial-guess 1d0) :then (average guess next)
:for next = (funcall fn guess)
:until (close-enough? guess next)
:finally (return next))))
Using the Fixed Point function to find k-th roots
Above, we showed that the square root of 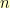 is a fixed point of the function
is a fixed point of the function 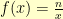 . Now, we can use that to write our own square root function:
. Now, we can use that to write our own square root function:
(defun my-sqrt (n)
(fixed-point (lambda (x) (/ n x)))
By the same argument we used with the square root, we can find the 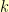 -th root of 5 by finding the fixed point of
-th root of 5 by finding the fixed point of 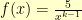 . We can make a function that returns a function that does k-th roots:
. We can make a function that returns a function that does k-th roots:
(defun kth-roots (k)
(lambda (n)
(fixed-point (lambda (x) (/ n (expt x (1- k)))))))
(setf (symbol-function 'cbrt) (kth-root 3))
Inverting functions
I found myself wanting to find inverses of various complicated functions. All that I knew about the functions was that if you restricted their domain to the unit interval, they were one-to-one and their domain was also the unit interval. What I needed was the inverse of the function.
For some functions (like 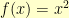 ), the inverse is easy enough to calculate. For other functions (like
), the inverse is easy enough to calculate. For other functions (like 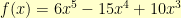 ), the inverse seems possible but incredibly tedious to calculate.
), the inverse seems possible but incredibly tedious to calculate.
Could I use fixed points to find inverses of general functions? We’ve already used them to find inverses for 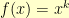 . Can we extend it further?
. Can we extend it further?
After flailing around Google for quite some time, I found this article by Chen, Lu, Chen, Ruchala, and Olivera about using fixed-point iteration to find inverses for deformation fields.
There, the approach to inverting 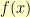 was to formulate
was to formulate 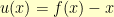 and let
and let 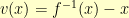 . Then, because
. Then, because
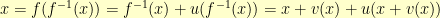
That leaves the relationship that
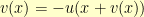
. The goal then is to find a fixed point of
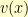
.
I messed this up a few times by conflating 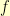 and
and  so I abandoned it in favor of the tinkering that follows in the next section. Here though, is a debugged version based on the cited paper:
so I abandoned it in favor of the tinkering that follows in the next section. Here though, is a debugged version based on the cited paper:
(defun pseudo-inverse (fn &optional (tolerance 1d-10))
(lambda (x)
(let ((iterant (lambda (v)
(flet ((u (x)
(- (funcall fn x) x)))
(- (u (+ x v)))))))
(+ x (fixed-point iterant 0d0 tolerance)))))
Now, I can easily check the average variance over some points in the unit interval:
(defun check-pseudo-inverse (fn &optional (steps 100))
(flet ((sqr (x) (* x x)))
(/ (loop :with dx = (/ (1- steps))
:with inverse = (pseudo-inverse fn)
:repeat steps
:for x :from 0 :by dx
:summing (sqr (- (funcall fn (funcall inverse x)) x)))
steps)))
(check-pseudo-inverse #'identity) => 0.0d0
(check-pseudo-inverse #'sin) => 2.8820112095939962D-12
(check-pseudo-inverse #'sqrt) => 2.7957469632748447D-19
(check-pseudo-inverse (lambda (x) (* x x x (+ (* x (- (* x 6) 15)) 10))))
=> 1.3296561385041381D-21
A tinkering attempt when I couldn’t get the previous to work
When I had abandoned the above, I spent some time tinkering on paper. To find 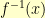 , I need to find
, I need to find 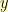 so that
so that 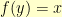 . Multiplying both sides by
. Multiplying both sides by 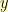 and dividing by
and dividing by 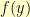 , I get
, I get 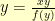 . So, to find
. So, to find 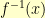 , I need to find a
, I need to find a 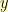 that is a fixed point for
that is a fixed point for 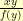 :
:
(defun pseudo-inverse (fn &optional (tolerance 1d-10))
(lambda (x)
(let ((iterant (lambda (y)
(/ (* x y) (funcall fn y)))))
(fixed-point iterant 1 tolerance))))
This version, however, has the disadvantage of using division. Division is more expensive and has obvious problems if you bump into zero on your way to your goal. Getting rid of the division also allows the above algorithms to be generalized for inverting endomorphisms of vector spaces (the 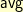 function being the only slightly tricky part).
function being the only slightly tricky part).
Denouement
I finally found a use of the fixed-point function that goes beyond 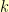 -th roots. Wahoo!
-th roots. Wahoo!
and with
less than
then unit spheres at those locations would overlap each other). If I keep (n-1) of the coordinates rational, the n-th coordinate will be the square root of a rational number.

