CL-FFT v1.4.2011.03.24 released March 24th, 2011
Patrick Stein

Elliott Johnson provided me with some patches for my CL-FFT library so that it will work with Allegro modern mode (mlisp).

Thank you!

Tutorial: Introduction to Conditions and Restarts March 18th, 2011
Patrick Stein

Today was the first time that I really kicked the tires on Common Lisp’s conditions and restarts. I thought that I’d share some of the experience as a sort of mini-tutorial. This tutorial assumes some minimal experience hitting the debugger from the REPL and some comfort with CLOS.

Lisp: Conditions and Restarts from Patrick Stein on Vimeo.

Screencast tutorial on basic conditions and restarts in Common Lisp.

Here is the source code generated during this tutorial.

USerial Library — v0.3.2011.03.05 March 4th, 2011
Patrick Stein

I have released a new version of my serialization library. I hope no one has dug in too far on using it yet because I rearranged the interface a fair bit in this release. To accommodate more complex serializers and unserializers as well as supporting a with-buffer macro, the buffer is no longer the first argument to the serialize and unserialize methods. Now, it is a &key argument to the serialize and unserialize generics. Further, the serialize and unserialize generics also &allow-other-keys.

In an intervening and unannounced release, I added serializers for slots and accessors.

In this release, I have also really fleshed out the documentation and examples.

For instructions on obtaining and using the USerial library, please refer to the USerial library web page.

Edit: This had been v0.3.2011.03.04, but I made a minor update to add MIT License and correct a few glitches in the docs. Now, it’s v0.3.2011.03.05.

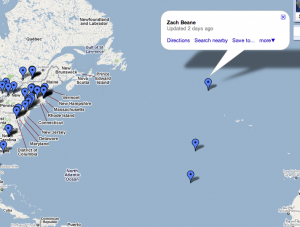
Swim, Zach! Swim! February 26th, 2011
Patrick Stein

It looks like Google Maps is having some longitude problems along the eastern coast of the U.S. This is from the CL-USERS Google Map:

Calculating the mean and variance with one pass February 15th, 2011
Patrick Stein

A friend showed me this about 15 years ago. I use it every time I need to calculate the variance of some data set. I always forget the exact details and have to derive it again. But, it’s easy enough to derive that it’s never a problem.

I had to derive it again on Friday and thought, I should make sure more people get this tool into their utility belts.

First, a quick refresher on what we’re talking about here. The mean \mu of a data set { x_1, x_2, \ldots, x_n } is defined to be \frac{1}{n} \sum_{i=1}^n x_i. The variance \sigma^2 is defined to be \frac{1}{n} \sum_{i=1}^n (x_i - \mu)^2.

A naïve approach to calculating the variance then goes something like this:

(defun mean-variance (data)
  (flet ((square (x) (* x x)))
    (let* ((n (length data))
           (sum (reduce #'+ data :initial-value 0))
           (mu (/ sum n))
           (vv (reduce #'(lambda (accum xi)
                           (+ accum (square (- xi mu))))
                       data :initial-value 0)))
      (values mu (/ vv n)))))

This code runs through the data list once to count the items, once to calculate the mean, and once to calculate the variance. It is easy to see how we could count the items at the same time we are summing them. It is not as obvious how we can calculate the sum of squared terms involving the mean until we’ve calculated the mean.

If we expand the squared term and pull the constant \mu outside of the summations it ends up in, we find that:

\frac{\sum (x_i - \mu)^2}{n} = \frac{\sum x_i^2}{n} - 2 \mu \frac{\sum x_i}{n} + \mu^2 \frac{\sum 1}{n}

When we recognize that \frac{\sum x_i}{n} = \mu and \sum_{i=1}^n 1 = n, we get:

\sigma^2 = \frac{\sum x_i^2}{n} - \mu^2 = \frac{\sum x_i^2}{n} - \left( \frac{\sum x_i}{n} \right)^2
.

This leads to the following code:

(defun mean-variance (data)
  (flet ((square (x) (* x x)))
    (destructuring-bind (n xs x2s)
        (reduce #'(lambda (accum xi)
                    (list (1+ (first accum))
                          (+ (second accum) xi)
                          (+ (third accum) (square xi))))
                data :initial-value '(0 0 0))
      (let ((mu (/ xs n)))
        (values mu (- (/ x2s n) (square mu)))))))

The code is not as simple, but you gain a great deal of flexibility. You can easily convert the above concept to continuously track the mean and variance as you iterate through an input stream. You do not have to keep data around to iterate through later. You can deal with things one sample at a time.

The same concept extends to higher-order moments, too.

Happy counting.

Edit: As many have pointed out, this isn’t the most numerically stable way to do this calculation. For my part, I was doing it with Lisp integers, so I’ve got all of the stability I could ever want. 🙂 But, yes…. if you are intending to use these numbers for big-time decision making, you probably want to look up a really stable algorithm.

RSS Feeds

l