Fog of Light – Getting Underway May 15th, 2017
Patrick Stein

Dauntless (The Lost Fleet, Book 1) was the first science-fiction book I read that tried to deal with space combat with the real-world constraint that light only travels so fast. It takes light eight minutes to get from the Sun to Earth. It takes light more than a second to get from the Earth to the Moon. Depending on where they are in their orbits, it takes between three minutes and twenty-two minutes to get light from Mars to Earth.

Imagine that you’re a star-ship. You and your companions have just warped into a new star system. You see a flotilla of enemy ships about 45 light-minutes away. That means, you’ve got 45 minutes before that flotilla can possibly even know that you’re in their star system. How much can you get done in that time? Once they can see you, how much can you mislead them on your target if they’re going to be operating on data about where you were heading more than half an hour ago?

For years, I have been batting around this concept, hammering it into a game. I have finally gotten started on it.

Armed with some functions like these, I am constructing values which change at points in space-time and querying the value visible from other points in space-time.

(defgeneric get-nearest-value (space-time-value space-time-point)
  ...
  (:documentation "Find the observable value of a quantity
SPACE-TIME-VALUE when observed from a given location
SPACE-TIME-POINT. This method finds the most-recent
value V0 (at location P0) for this data when viewed from
the given location. This method returns (VALUES V0 P0).
This method makes no effort to interpolate the results."))

Here are my first, visually-demonstrable results:

Hopefully, there will be plenty more coming in the near future.

If it quacks like a parabola… September 21st, 2011
Patrick Stein

I am working on a game idea that involves (special) relativistic mechanics instead of classical mechanics. Working out the details that I needed was easy enough if I assumed that:

  • ships had a maximum speed at which they could move relative to my base frame
  • ships could instantly go from stopped to maximum speed or vice-versa

I didn’t like those assumptions at all. So, I started playing with the equations for relativity. In classical mechanics, the rate-of-change of velocity equals the force you’re applying divided by your mass: \frac{dv}{dt} = \frac{F}{m}.

In special relativity, your mass increases with velocity. So, that equation becomes: \frac{d\left(\frac{v}{\sqrt{1-v^2}}\right)}{dt} = \frac{F}{m_0} (assuming units where the speed of light is 1 unit of distance per 1 unit of time and m_0 is your rest-mass).

For the purposes of this post, I’m going to assume the simplest initial conditions: you start motionless and at the origin. For ease of notation, let a = \frac{F}{m_0}. Solving the above differential equation to get a formula for velocity and solving the resulting differential equation to get the distance x you’ve travelled in my base frame by time t, the answer comes out to: x(t) = \frac{1}{a}\left(-1 + \sqrt{1+a^2t^2}\right).

I have solved this problem at least thirty times in the past two months. Sometimes I used the simple initial conditions as above. Sometimes I did it in all of its gory details (including the messy case where the applied force is not aligned with the current velocity).

I got the same answer (well, plus the extra mess when I did the full-on problem) every way that I tried it.

So, why did I do it over and over again?

If this were classical mechanics, the end equation would have been x(t) = \frac{1}{2}at^2. And, I know that for low velocities, the classical mechanics answer should be almost identical to the special relativity answer. And, there was no way that I thought \frac{1}{a}\left(-1 + \sqrt{1+a^2t^2}\right) \approx \frac{1}{2}at^2.

I knew what the graph x = \sqrt{a^2t^2} looked like when t \ge 0. It is a straight line. It doesn’t look much like the parabola x = \frac{1}{2}a t^2 at all.

My assumption was that since x = \sqrt{a^2t^2} was a straight line for t \ge 0, then x = \sqrt{1 + a^2t^2} would be a straight line shifted up one unit and bent (concave-down) a little bit like the graph of x = \sqrt{at} is bent.

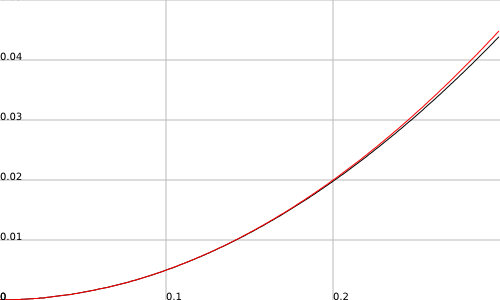
Boy was I wrong. Here is a plot of the two together (created with fooplot). The red line is the classical mechanics version. The black line is the relativistic version. Here, the force is such that the body is accelerating at a rate of the speed of light per second so they’ve already gotten up to around 28,000 miles per second before you can see any separation in the graphs here.

distance (in light-seconds) vs. time (in seconds)

Definitely, I can see the resemblance. Now, to fix my intuition about square-roots.

RSS Feeds

l