Motivation
I no longer remember what led me to this page of synthetic division implemented in various languages. The author provides a common lisp implementation for taking a list representing the coefficients of a polynomial in one variable 
and a number 
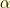and returning the result of dividing the polynomial by 
.
The author states: I’m very sure this isn’t considered Lispy and would surely seem like an awkward port from an extremely Algol-like mindset in the eyes of a seasoned Lisper.
In the mood for the exercise, I reworked his code snippet into slightly more canonical lisp while leaving the basic structure the same:
(defun synthetic-division (polynomial divisor)
(let* ((result (first polynomial))
(quotient (list result)))
(dolist (coefficient (rest polynomial))
(setf result (* result divisor))
(incf result coefficient)
(push result quotient))
(let ((remainder (pop quotient)))
(list :quotient (nreverse quotient) :remainder remainder))))
From there, I went on to implement it using tail recursion to get rid of the #'setf and #'incf and #'push:
(defun synthetic-division-2 (polynomial divisor)
(labels ((divide (coefficients remainder quotient)
(if coefficients
(divide (rest coefficients)
(+ (* divisor remainder) (first coefficients))
(list* remainder quotient))
(list :quotient (reverse quotient) :remainder remainder))))
(divide (rest polynomial) (first polynomial) nil)))
What I didn’t like about this was the complexity of calling the tail-recursive portion. If I just called it like I wished to (divide polynomial 0 nil) then I ended up with one extra coefficient in the answer. This wouldn’t do.
The Joke
There’s an old joke about a physicist, a biologist, and a mathematician who were having lunch at an outdoor café. Just as their food was served, they noticed a couple walk into the house across the street. As they were finishing up their meal, they saw three people walk out of that very same house.
The physicist said, We must have miscounted. Three must have entered before.
The biologist said, They must have pro-created.
The mathematician said, If one more person enters that house, it will again be empty.
The Anti-Cons
What I needed was a more-than-empty list. I needed a negative cons-cell. I needed something to put in place of the nil in (divide polynomial 0 nil) that would annihilate the first thing it was cons-ed to.
I haven’t come up with the right notation to make this clear. It is somewhat like a quasigroup except that there is only one inverse element for all other elements. Let’s denote this annihilator: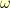 
. Let’s denote list concatenation with 
.
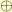Only having one inverse-ish element means we have to give up associativity. For lists 
and 
, evaluating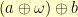 
equals , but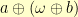 
equals .
Associativity is a small price to pay though for a prettier call to my tail-recursive function, right?
The Basic Operations
For basic operations, I’m going to need the anti-cons itself and a lazy list of an arbitrary number of anti-conses.
(defconstant anti-cons 'anti-cons)
(defclass anti-cons-list ()
((length :initarg :length :reader anti-cons-list-length))
(:default-initargs :length 1))
(defmethod print-object ((obj anti-cons-list) stream)
(print-unreadable-object (obj stream)
(prin1 (loop :for ii :from 1 :to (anti-cons-list-length obj)
:collecting 'anti-cons)
stream)))
Then, I’m going to make some macros to define generic functions named by adding a minus-sign to the end of a Common Lisp function. The default implementation will simply be the common-lisp function.
(defmacro defun- (name (&rest args) &body methods)
(let ((name- (intern (concatenate 'string (symbol-name name) "-"))))
`(defgeneric ,name- (,@args)
(:method (,@args) (,name ,@args))
,@methods)))
I’m even going to go one step further for single-argument functions where I want to override the body for my lazy list of anti-conses using a single form for the body:
(defmacro defun1- (name (arg) a-list-form &body body)
`(defun- ,name (,arg)
(:method ((,arg anti-cons-list)) ,a-list-form)
,@body))
I need #'cons- to set the stage. I need to be able to cons an anti-cons with a normal list. I need to be able to cons an anti-cons with a list of anti-conses. And, I need to be able to cons something other than an anti-cons with a list of anti-conses.
(defun- cons (a b)
(:method ((a (eql 'anti-cons)) (b list))
(if (null b)
(make-instance 'anti-cons-list)
(cdr b)))
(:method ((a (eql 'anti-cons)) (b anti-cons-list))
(make-instance 'anti-cons-list :length (1+ (anti-cons-list-length b))))
(:method (a (b anti-cons-list))
(let ((b-len (anti-cons-list-length b)))
(when (> b-len 1)
(make-instance 'anti-cons-list :length (1- b-len))))))
Now, I can go on to define some simple functions that can take either anti-cons lists or regular Common Lisp lists.
(defun1- length (a) (- (anti-cons-list-length a))
(defun1- car (a) :anti-cons)
(defun1- cdr (a)
(let ((a-len (anti-cons-list-length a)))
(when (> a-len 1)
(make-instance 'anti-cons-list :length (1- a-len)))))
(defun1- cadr (a) (when (> (anti-cons-list-length a) 1) :anti-cons))
(defun1- caddr (a) (when (> (anti-cons-list-length a) 2) :anti-cons))
To give a feel for how this all fits together, here’s a little interactive session:
ANTI-CONS> (cons- anti-cons nil)
#<(ANTI-CONS)>
ANTI-CONS> (cons- anti-cons *)
#<(ANTI-CONS ANTI-CONS)>
ANTI-CONS> (cons- :a *)
#<(ANTI-CONS)>
ANTI-CONS> (length- *)
-1
Denouement
Only forty or fifty lines of code to go from:
(divide (rest polynomial) (first polynomial) nil)
To this:
(divide polynomial 0 (cons anti-cons nil))
Definitely worth it.
-th column (or row) (for 
) represents 
for some generator 
in the zeroth row and column and 
for the spot 
.
on the right and 
on the left. They make as decent a stereo as any of the other pairs so far.
