Fun(??) with Backups August 13th, 2009
Patrick Stein

I live each day with the fear of a catastrophic disk crash.

Most of the data I care about lives on my MacBook Pro. My PowerBook had some disk drive issues at one point. Because it had been a month since I had backed it up, and that backup was partially scrogged, I lost about six weeks of work when that drive flipped out.

I mitigate this slightly by mirroring my VCS repositories to several different machines. I also download digital images to two different computers before deleting them from the camera. I still suffer through Retrospect backing up to DVD-R every few weeks.

I recorded the presentations from the last TC Lispers meeting. I expect to do the same at this month’s meeting. Because the raw material from last month was 48GB and because I only had about 45GB of space remaining on my drive, I needed to get that 48GB out of the way by next week. So, I was caught in a crisis.

It’s not data that I want to pay $0.15/GB/month to store. It’s not data that I just want to throw away. At the same time, I am probably not going to need that raw data again for at least a year.

After struggling through the first six disks (which took me eleven disks) trying to backup the data to DVD-R with Retrospect and having only backed up about a quarter of my data at this point, I abandoned trying to write use Retrospect to archive the data. So, now what?

Problems I Would Like to Solve

  • Day-to-day Peace-of-mind: If my drive crashes, I haven’t lost too much time or irreproducible data
  • Archival: There is some data I don’t want to throw away, but don’t need spinning next to me
  • Fire-safety: If a small nuclear device explodes in my computer corner, I haven’t lost too much time or irreproducible data

My solutions

I have added two 1TB disks to my Linux box. I have set these up as a RAID-1 (technically, as a RAID-5 with one faulty-by-way-of-being-absent drive). I have set this filesystem up to be shared via Appletalk, and I have set up Time Machine on my Mac to backup onto that filesystem. Turning on Time Machine was a significant pain. The how-to page is wonderful. However, File Vault and Time Machine don’t play nicely together. Turning off File Vault was terribly annoying. I will tell you more about that below.

So, this takes care of my Day-to-day Peace-of-mind. It has also given me a stop-gap on the Archival. I have a fair bit of space at the moment to drop 48GB. It’s spinning, but it isn’t costing me $7/month either.

I still have Fire-Safety to deal with. I have a 250GB external drive. I will probably use SuperDuper! or one of its cohorts to back up to that external drive. Then, I can lock the drive in the firebox or take it offsite. I will have to find some way to get backups from my Linux box onto the drive, too, but that seems fairly tractable.

For longer term Archival, I am going to give ArchiveMac a shot.

If I find a good archival solution, then I may go with one of the online backup services for my Fire-Safety and/or Day-to-Day Peace-of-Mind.

If any of y’all have a good Archival or Fire-Safety strategy, I’d love to hear it.

The Problems that I’ve had with Retrospect

Note: I am using Retrospect 6 even though they are currently on 8. I do not like 6 so I can’t imagine paying them more money.

I bought six because it was the only software I could find at the time that allowed me to do full and incremental backups and backup to DVD. Actually, it turns out that it would only let me have full flexibility on the full/incremental stuff if I backed up to big media. To do things to DVD, I couldn’t branch arbitrarily and do an incremental based on a chosen previous backup in the same heritage.

Even worse, Retrospect is very picky about both the drive and the media. I made many coasters trying to get backups working at all. Even when they were working, about three in eight disks were coasters before it even finished writing them. Of those it finished writing, about one in twelve were coasters-in-hiding.

Combining the coasters-in-hiding problem with the unable to pick the parent for my backup meant that if I didn’t do the backup with verification turned on, I couldn’t come back later and re-do the backup. Retrospect would consider that backup complete. If it wasn’t, then I had to go through and touch any files that I wanted to make sure got backed up on my next attempt.

The Problem with Time Machine and File Vault

I didn’t turn on Time Machine when I first upgraded to Leopard. I didn’t do this because Time Machine has no subtlety. It will keep that 48GB of data I may never need spinning and spinning. When Time Machine runs out of space, it starts getting rid of the oldest stuff. As such, until I run out of space, I’ve got this 48GB I may never need. Once it runs out of space, I don’t have old versions of things that have changed recently. It’s a nice Day-to-Day Peace-of-Mind, but it is not an Archival solution.

Early this year sometime, I turned on File Vault. There shouldn’t be anything particularly sensitive on my drive outside of my Keychain. On the other hand, there’s no reason someone stealing my laptop should get to have any of it. It seemed like an easy win.

Then, I went to turn on Time Machine yesterday. Time Machine warned me that my home directory was encrypted. As such, it could not backup my home directory as individual files. It could only back up my home directory as a whole. And, it could only do this when I am not logged in. When I am at home (which would be the only time I have access to the external drives that I’d be using Time Machine on anyhow), I am always logged in. I don’t want to have to restore my whole home directory somewhere to get back a file I shouldn’t have deleted. I would much rather it backs things up only when I am logged in. How often do my files change when I am not changing them?

Fine, I’ll turn off File Vault. That wasn’t so easy. File Vault wanted me to free up 128GB of space on my home volume so it could decrypt itself. I only had about 70GB of space available.

I had to back some stuff up so I could delete it so I could make enough room to turn off File Vault so I could turn on backup software! It’s brilliant, brilliant, brilliant!

I moved the 48GB of raw presentations over to the RAID on the Linux box. This took about 45-minutes. Then, I moved my iTunes Music and my VMWare disk images out of my home directory. This took about an hour.

Unfortunately, since File Vault was keeping my home directory as a Sparse Bundle on my main drive, moving things out of the Sparse Bundle and onto the main drive didn’t free up any space inside the Sparse Bundle. Thinking it would be faster to move stuff to a locally connected FireWire drive than over the network to the RAID, I deleted the 200GB of Retrospect backup catalogs that I had on the external drive and moved my iTunes Music and VMWare disk images over there instead. This took another hour.

Finally, I got to turn off File Vault. I didn’t wait around for it to figure out how long it thought it would take. It took more than half an hour and less than an hour-and-a-half for it to finish that.

Then, I moved my iTunes Music and VMWare disk images back from the external drive (another 45-minutes or more).

Then, finally, I turned on Time Machine.

I spent more time turning off File Vault and turning on Time Machine than I did buying disks, creating the RAID, setting up Appletalk under Linux, and plopping the 48GB of raw presentations across a network onto the RAID.

Ask a simple question… August 8th, 2009
Patrick Stein

Ask a simple question, spend the next forty minutes sifting through integral tables. Earlier, I took some code that was uniformly selecting points from a square centered at the origin and converted it to code using points from a normal distribution. For my purposes, I used a standard-deviation for the normal distribution that was half of the in-radius of the box. It wasn’t at all exact in any way.

What if I wanted to be exact? Suppose I wanted to switch from points uniformly distributed in a box to points from a normal distribution while maintaining the expected distance from the selected point to the origin.

What exactly is the expected distance from a selected point to the origin if one picks each coordinate for the point from a uniform distribution on the range [-1,+1]? Let’s start with the one-dimensional case. The probability density is \frac{1}{2} everywhere. So, the answer is 2 \int_{r=0}^1 \frac{1}{2} r dr = \frac{1}{2} as we would expect.

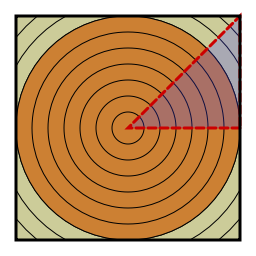(image created in Lisp using Zach's Vecto library)How about two dimensions? This is immediately more awkward. The one-dimensional disk looks exactly like the one-dimensional square. In two dimensions, the disk and square are quite different. We either have to integrate over the square and calculate the radius of each point, or we have to integrate over increasing radii and be careful once we get to the in-radius of the square. (image created in Lisp using Zach's Vecto library)

I originally chose to try to integrate over the square. The probability density is \frac{1}{4} everywhere. This means the expected radius is \int_{y=-1}^1 \int_{x=-1}^1 \sqrt{x^2+y^2} dx dy. This gets to be no fun very fast since the inner integral comes out with a logarithm in it. I mean, do you want to finish this integral?

\int_{y=-1}^1 \left.\left( \frac{1}{2} x \sqrt{x^2 + y^2} + \frac{1}{2} y^2 \ln \left( x + \sqrt{x^2 + y^2} \right)\right)\right|_{x=-1}^1 dy

It may be easy. I didn’t want to mess with it. I suppose once you evaluate the x terms, it reduces a fair bit (if I did that all right):
\int_{y=-1}^1 \left( \sqrt{1 + y^2} + \frac{1}{2} y^2 \ln \left( \frac{1 + \sqrt{1 + y^2}}{-1 + \sqrt{1 + y^2}} \right) \right) dy

I still don’t want to touch it.

So, how about integrating over the radii? Again, the probability density is \frac{1}{4} everywhere. This makes the expected radius:

\int_{r=0}^1 \frac{1}{4} \cdot 2 \pi r dr + \int_{r=1}^{\sqrt{2}} \frac{1}{4} \cdot 8 \left( \frac{\pi}{4} - \arccos \frac{1}{r} \right) dr

With a little massaging, you can move the \frac{\pi}{4} from the second integral into the first instead:
\int_{r=0}^{\sqrt{2}} \frac{1}{4} \cdot 2 \pi r dr - \int_{r=1}^{\sqrt{2}} \frac{1}{4} \cdot 8 \arccos \frac{1}{r} dr

This is hardly consolation though. Here is where we get lost in our table of integrals for the better part of an hour.

And, this is only the two-dimensional case! In my original problem, the ambient space was 32-dimensional. My, oh my.

Axiom of Choice Joke: Now for Sale August 7th, 2009
Patrick Stein

There’s an old math joke that goes like this: The Axiom of Choice is obviously true. The Well-Ordering Theorem is obviously false. And, Zorn’s Lemma is just too complicated to be sure. It is a joke because it is easy to prove that they are equivalent.

MathSignLang For a month now, I have wanted to turn that joke into a Sign Language for Mathematicians picture. I finally got to it this evening. You can see the result on the right.

You can purchase it on a t-shirt or mug over at Zazzle, if you like.

The intuition

I am going to try to paraphrase the Axiom of Choice, the Well-Ordering Theorem, and Zorn’s Lemma to try to give you a sense of why each statement in the joke seems intuitively correct.

Suppose that I have infinitely many boxes. Each box contains one red ball and one blue ball. You can, with or without the Axiom of Choice, pick one ball from each box unless you are colorblind. If you are colorblind, you need the Axiom of Choice to pick one ball from each box even if you don’t care what color that ball is. What a wacky world it would be if a colorblind person could not pick a ball from each of these boxes. So, obviously, the Axiom of Choice should be true.

Suppose you have all of the real numbers from zero to one including both zero and one. If I asked you to give me the smallest number you’ve got, you could hand me the zero. Now, if I asked you to give me the smallest number you’ve got, you’re stuck. What the Well-Ordering Theorem says is that there is some way we could sort your collection of numbers so that no matter how many of them I take away (so long as I don’t take them all), you will never get stuck. It seems crazy that you can just shuffle your collection of numbers to keep me from thwarting you.

As the joke mentions, Zorn’s Lemma is complicated. On the one hand, Zorn’s Lemma says that if you took the genealogy of all people born in the last 8,000 years, then there exists at least one person with no ancestors born in the last 8,000 years. On the other hand, Zorn’s Lemma says that you didn’t need to shuffle your numbers so that you could still give me the smallest number in your hand after I took away the zero.

How it looks on a t-shirt

Casting to Integers Considered Harmful August 6th, 2009
Patrick Stein

Background

Many years back, I wrote some ambient music generation code. The basic structure of the code is this: Take one queen and twenty or so drones in a thirty-two dimensional space. Give them each random positions and velocities. Limit the velocity and acceleration of the queen more than you limit the same for the drones. Now, select some point at random for the queen to target. Have the queen accelerate toward that target. Have the drones accelerate toward the queen. Use the average distance from the drones to the queens in the i-th dimension as the volume of the i-th note where the notes are logarithmically spaced across one octave. Clip negative volumes to zero. Every so often, or when the queen gets close to the target, give the queen a new target.

It makes for some interesting ambient noise that sounds a bit like movie space noises where the lumbering enemy battleship is looming in orbit as its center portion spins to create artificial gravity within.

I started working on an iPhone application based on this code. The original code was in C++. The conversion to Objective C was fairly straightforward and fairly painless (as I used the opportunity to try to correct my own faults by breaking things out into separate functions more often).

Visualization troubles

uniform
The original code though chose random positions and velocities from uniform distributions. The iPhone app is going to involve visualization as well as auralization. The picture at the right here is a plot of five thousand points with each coordinate selected from a uniform distribution with range [-20,+20]. Because each axis value is chosen independently, it looks very unnatural.

gauss
What to do? The obvious answer is to use Gaussian random variables instead of uniform ones. The picture at the right here is five thousand points with each coordinate selected from a Gaussian distribution with a standard-deviation of 10. As you can see, this is much more natural looking.

How did I generate the Gaussians?

I have usually used the Box-Muller method of generating two Gaussian-distributed random variables given two uniformly-distributed random variables:

(defun random-gaussian ()
  (let ((u1 (random 1.0))
        (u2 (random 1.0)))
    (let ((mag (sqrt (* -2.0 (log u1))))
          (ang (* 2.0 pi u2)))
      (values (* mag (cos ang))
              (* mag (sin ang))))))

But, I found an article online that shows a more numerically stable version:

(defun random-gaussian ()
  (flet ((pick-in-circle ()
           (loop as u1 = (random 1.0)
                as u2 = (random 1.0)
                as mag-squared = (+ (* u1 u1) (* u2 u2))
                when (< mag-squared 1.0)
                return (values u1 u2 mag-squared))))
    (multiple-value-bind (u1 u2 mag-squared) (pick-in-circle)
      (let ((ww (sqrt (/ (* -2.0 (log mag-squared)) mag-squared))))
        (values (* u1 ww)
                (* u2 ww))))))

For a quick sanity check, I thought, let’s just make sure it looks like a Gaussian. Here, I showed the code in Lisp, but the original code was in Objective-C. I figured, If I just change the function declaration, I can plop this into a short C program, run a few thousand trials into some histogram buckets, and see what I get.

The trouble with zero

So, here comes the problem with zero. I had the following main loop:

#define BUCKET_COUNT 33
#define STDDEV       8.0
#define ITERATIONS   100000

  for ( ii=0; ii < ITERATIONS; ++ii ) {
    int bb = val_to_bucket( STDDEV * gaussian() );
    if ( 0 <= bb && bb < BUCKET_COUNT ) {
      ++buckets[ bb ];
    }
  }

I now present you with three different implementations of the val_to_bucket() function.

int val_to_bucket( double _val ) {
  return (int)_val + ( BUCKET_COUNT / 2 );
}

int val_to_bucket( double _val ) {
  return (int)( _val + (int)( BUCKET_COUNT / 2 ) );
}

int val_to_bucket( double _val ) {
  return (int)( _val + (int)( BUCKET_COUNT / 2 ) + 1 ) - 1;
}

As you can probably guess, after years or reading trick questions, only the last one actually works as far as my main loop is concerned. Why? Every number between -1 and +1 becomes zero when you cast the double to an integer. That’s twice as big a range as any other integer gets. So, for the first implementation, the middle bucket has about twice as many things in it as it should. For the second implementation, the first bucket has more things in it than it should. For the final implementation, the non-existent bucket before the first one is the overloaded bucket. In the end, I used this implementation instead so that I wouldn’t even bias non-existent buckets:

int val_to_bucket( double _val ) {
  return (int)lround(_val) + ( BUCKET_COUNT / 2 );
}

RSS Feeds

l