nklein software

Edit: lispnik on Livejournal pointed out this section of the Hyperspec which gaurantees that my pointer math is valid. I’d still like to know how to make a closure like this though, for future reference.

Edit(2): See tfb’s comment below for a solution that does make a closure using a nested (LAMBDA …) inside the backquote.

My Fast Fourier Transform library operates on multi-dimensional arrays. When you do a Fourier Transform on a two-dimensional array, you do a Fourier Transform on each row and then on each column of the result (or each column and then on each row of the result). When you do a three-dimensional Fourier Transform, you do a two-dimensional Fourier Transform on each horizontal slice and then a one-dimensional Fourier Transform on each vertical column.

The problem

To accomplish this on arrays of any number of dimensions, I wrote a wrapper class called virtual-row that one can use to index any axis-parallel row in a data hypercube with an API that makes it look like a one-dimensional array. So, for example, if I had a four-dimensional array, zero-ing one of those rows explicitly might look like this:

In my abstracted world, it would look like this:

A simple, straightforward implementation of the virtual row setter function might look like this:

The problem with that implementation is that it allocates a new list every time. This function is called 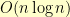times per row (and there are 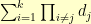virtual rows in a 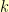-dimensional hypercuboid where the 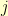-th dimension has 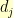entries).

The Goal

What I wanted to do instead was to generate a closure that incorporated the pre and post lists. What I wanted was almost this:

I say almost because (EVAL …) occurs in the null lexical environment. This means that it doesn’t capture the array variable. If I put a comma in front of the array, then I get a representation of the value to which array is bound, which doesn’t help me. Nor does passing in ’array since array is a lexical variable where I’m calling it from, too.

Putting the (EVAL …) inside the (LAMBDA …) doesn’t help because then it happens at runtime and I just spend all of my time in crazy functions like (APPEND …) and (READ-FROM-STRING …).

I tried assembling a list by hand instead of with the backquote. This was hampered both by the fact that (LAMBDA …) is a macro and because I still couldn’t capture a lexical variable (only its value). Other attempts that lead nowhere are:

The (READ-FROM-STRING …) tells me that AA is UNBOUND. This is unsurprising. Why should it care about my current lexical environment?

The (MACROEXPAND …) gives me a fabulous message under SBCL:

It seems like it might be slightly possible to work something out with an extra macro-level and some use of the &ENVIRONMENT lambda list keyword. But, I am not even sure where to start trying to figure out how that all plays together.

The Hack

Having failed to make a good closure on the fly and not being interested in consing as much as the simple implementation above does, I have settled instead for cheating. Here is how I am cheating.

The idea here is to compute the difference in (ARRAY-ROW-MAJOR-INDEX …) between the first and second elements in the row. (Note: the whole business with (MIN …) is to avoid trouble if there is no second element in the row.) Then, I assume that the 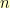-th element of the row will be 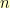times that difference beyond the initial element of the row.

This works well and quickly. But, it is somewhat cheesy. There is no requirement that my index math be correct for any given implementation. It would shock me to find that some implementation disagreed with the above index math. Still, I’d really like to just fabricate a proper closure around (AREF …) instead.

Can anyone lend me a half a cup of clue?